Tre geometriska problem

Personligen tycker jag att matematik är som bäst när enkla, okomplicerade frågor leder till avancerade resonemang som till slut blir till lika enkla, eleganta svar. Sådana problem var exempelvis de antika grekerna mästare på att formulera – utan avancerade beräkningsmodeller, numeriska metoder med oändligt många steg eller axiom som strider mot all mänsklig intuition. Tre sådana problem, typiska för den grekiska matematiken, har blivit berömda på grund av sin skenbara enkelhet. Alla skulle lösas med endast passare och onumrerad linjal.

De tre geometriska problemen är alla känneteckna de för den grekiska matematiken, men i många fall är deras exakta uppkomst höljd i historiens dimma. Hippokrates, känd för sina insatser på medicinens område men även som författare till matematiska verk, står bakom en berömd sammanställning av problemen. Här ses ruinerna efter läkekonstens tempel, Asklepieion, på hans hemö Kos. Foto: Wikimediaanvändare Cup of coffee, CC-BY-SA 3.0

1. Vinkelns tredelning eller att dela en vinkel i tre lika delar
Att dela en vinkel i två lika stora vinklar är relativt enkelt, till och med med de sparsmakade verktyg grekerna ställde till vårt förfogande - man kan rent av bevisa att alla vinklar går att dela på mitten med de förutsättningarna. Att dela samma vinkel i tre lika stora delar är desto mer utmanande. Bortsett från ett antal speciella vinklar (3π/2, 9π/4, ja, alla som är en jämn tre-multipel av en konstruerbar vinkel) så krävs för tredelning av en vinkel ett speciellt villkor, som grekerna hade lika svårt för som de hade för siffran noll: Oändligheten.

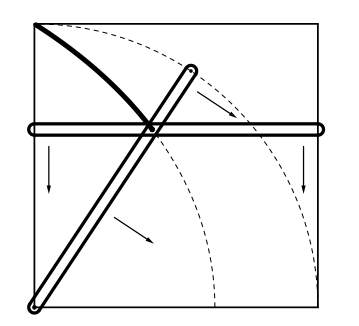
Vem som först formulerade problemet med vinkelns tredelning är inte känt. Hippokrates, som intresserade sig för de tre problemen, visade däremot att det är möjligt att dela vilken vinkel som helst i tre delar om man har tillgång till en linjal med avståndsmarkeringar. En vinkel CAB kan då med tre steg delas i tre delar:

1. Dra ett streck rakt ned från C, så att det skär linjen AB i punkten D.
2. Fortsätt så att en rektangel bildas, genom att rita till linjerna CF och AF.
3. Rita ett streck AE, så att CHG och CGE blir likbenta trianglar, och HG, GC och GE lika långa som AC. Vinkeln BAG är nu en tredjedel av CAB.

En utförlig beskrivning av Hippokrates lösning på problemet, tillsammans med andra berömda matematikers lösningar, som Arkimedes, Nicomedes och Apollonius, står att finna på den här sidan.

Antagligen var det just eftersom problemet var så lätt att lösa med en numrerad linjal, som det ursprungliga problemet att dela vinkeln med endast en omarkerad linjal sällan fick någon uppmärksamhet. 1837 publicerade fransmannen Pierre Wantzel ett bevis för att det är omöjligt. Även om vissa vinklar går att dela i tre, finns ingen metod som kan dela alla vinklar, så till vida att man inte kan tänka sig att hålla på i all oändlig framtid. Vi som inte vill det får helt enkelt nöja oss med att tredelning är en redigt svår nöt att knäcka.

Problemet med tredjedelar återfinns redan i den mesopotamiska historien om Gilgamesh, som sades vara två tredjedelar gud och en tredjedel människa. Tror man att babylonierna visste om att det krävs oändligt många generationer för att åstadkomma det kan man tolka det som en subtil symbol för, exempelvis, att gudaätten skulle vara oändlig. Tror man inte på den tolkningen, så framstår det som att även de bästa kan göra matematiska felsteg, och att vissa felsteg verkar kunna leva kvar i tusentals år.

2. Cirkelns kvadratur eller att skapa en cirkel med samma area som en kvadrat
Det andra problemet är utan tvivel det äldsta av de tre - intresset för cirkelns area är lika gammalt som civilisationen själv. Svårigheten att från en cirkel skapa en kvadrat med lika stor area är ju ett problem som möter varje person som vill beräkna en cirkels area, eftersom alla areor jämförs i termer av kvadrater (vilket ju är varför vi överhuvudtaget talar om kvadratmetrar).

Den egyptiske skrivaren Ahmes, som står som författare till den berömda Rhindpapyrusen, lär ha givit anvisningen att ta bort en niondel från cirkelns radie och därefter konstruera en kvadrat med den sidan, men den förste som gav sig på att lösa problemet mer exakt var greken Anaxagoras, som enligt den alltid så välinformerade Plutarchos lär ha sysselsatt sig med problemet under tiden han satt i fängelse. Problemet var tydligen populärt bland de antika grekerna, såväl bland matematiker som icke-matematiker - faktum är att det omnämns i den samtida teaterpjäsen Fåglarna av Aristofanes.

Ifall Anaxagoras kom till någon slutsats är inte längre känt. Problemet blev under tiden mycket omtyckt i Grekland, men likväl upptäcktes ingen elegant och enkel lösning på problemet, som bara använde en omärkt linjal och passare. Faktum är att det gick så långt att grekerna började använda beteckningen cirkelkvadrerare för alla dem som utan framgång försöker göra det omöjliga.

Det intressanta med den här tidens lösningar på problemet är att de gick ut på att fylla cirkeln med trianglar eller rektanglar av allt mindre storlek - till slut, tänkte man sig, skulle månghörningen helt fylla cirkeln. Därefter var det lätt att sätta samman dem till en kvadrat och därmed ha löst problemet. Även om metoden fick kritik inte minst från Aristoteles, kan vi i efterhand konstatera att den egentligen var långt före sin tid. Tanken att en area kan beräknas genom att fylla den med oändligt många regelbundna rektanglar och trianglar av allt mindre storlek är inte många steg från 1600-talets integralkalkyl.

En av dem som konstruerade en sådan lösning var filosofen och retorikern Antifon från Aten. Han började med att placera en så stor kvadrat som möjligt i mitten av cirkeln, och fyllde därefter på med allt mindre rätvinkliga trianglar. Metoden återanvändes långt senare av Arkimedes för att ge ett närmevärde till π.

Antifon trodde att [cirkelns] area på detta sätt skulle fyllas, varför vi vid något tillfälle skulle ha en månghörning inskriven i cirkeln, med så små sidor att de skulle sammanfalla med cirkelns omkrets. Och, eftersom vi redan till varje månghörning kan skapa en lika stor kvadrat ... kan vi då också skapa en kvadrat lika stor som en cirkel.” - Simplikios från Kilikien

Staden Elis ligger i en dalgång på Peloponnesos västkust och var hemstaden för Hippias, vars bidrag till matematiken bland annat inkluderade den geniala quadratrix-kurvan med vars hjälp problemet med cirkelns kvadratur nästan kunde lösas. Till staden hörde även antikens Olympia, platsen för de antika olympiska spelen. Här ses den valvförsedda ingången till den antika arenan. Foto: Troy McKaskle, CC-BY-SA 2.0

Det stora genombrottet i lösningen av cirkelns kvadratur kom med matematikern och filosofen Hippias från Elis. Kring år 420 f.Kr. konstruerade han en kurva, som senare har kommit att bli känd som Hippias quadratrix, med vars hjälp han kunde härleda en lösning till problemet med vinkelns tredelning. Någon generation senare visade Deinostratos, en av Platons lärjungar, att den gick att använda även till att lösa problemet med cirkelns kvadratur. Haken med den här metoden var att quadratrixen i sig inte kunde konstrueras med enbart en passare och en omärkt linjal.

För att konstruera Hippias quadratrix behövdes ett särskilt instrument, som bestod av två stavar och en kvadrat. Den ena staven satt fast i kvadratens sidor, på så sätt att den kunde skjutas uppåt och nedåt, medan den andra var fäst i ett av hörnen och med en glidande infästning i den andra staven. Skärningspunkten mellan dem skapade quadratrixen. Bild: Wikimediaanvändar Kmhkmh, CC-BY-SA 3.0

Kan vi med dagens matematik till hjälp lösa problemet med cirkelns kvadratur? För att göra det, behöver vi först betrakta proportionen mellan en kvadrats sida och en cirkels radie. En kvadrat med sidan s har arean s², medan en cirkel med radien r har arean πr². Om vi vill skapa en cirkel med samma area som en kvadrat, får vi först sätta areorna lika, d.v.s.

För att få fram cirkelns radie måste alltså sträckan delas med kvadratroten ur π. Problemet är att roten ur π, liksom π självt, är tal går inte att skapa med de verktyg som grekerna ställde till vårt förfogande. På ett sätt var det just det problemet var det som Arkimedes mötte på, och anledning till att han använde Antifons metod för att skapa en approximation till π. Ytterst beror det på att π är ett s.k. transcendent tal, något som bevisades av matematikern Ferdinand von Lindemann år 1882, vilket i korta ordalag betyder att det inte är en lösning till någon algebraisk ekvation - fast det är en annan historia.

3. Kubens fördubbling eller att bestämma sidan på en kub som är dubbelt så stor som en annan kub
Det tredje problemet är troligtvis det yngsta av de tre problemen. Uppgiften är att att till en kub med känd sida och volym skapa en kub med dubbla volymen. Ganska snart började dock problemet cirkulera i en mer generell form: Att till en given kub konstruera en ny kub, vars volym förhåller sig till den gamla kubens volym med samma proportion som två givna linjers längder förhåller sig till varandra.

Av de tre geometriska problemen var detta det under antiken mest berömda, fast var med anledning av en anekdot om när Aten drabbades av pesten känt som det deliska problemet. Den mest underhållande, men knappast sanningsenliga, versionen av anekdoten ger den hellenistiske matematikern Theon från Smyrna, som återberättar en historia från Eratosthenes numer förlorade verk Platonikos. Han berättar, att när Atens invånarna frågade oraklet på Delos hur de skulle bli av med pesten fick de svaret att de i Apollons, tillfrisknandets gud, tempel skulle konstruera ett nytt altare, som var dubbelt så stort som det gamla. Byggmästarna, vars uppgift ombyggnationen blev, hade ingen aning om hur de skulle gå till väga för att uppfylla gudens önskningar, och rådfrågade därför i sin förvirring Platon. Denne vise herre svarade att guden i själva verket inte alls var intresserad av ett dubbelt så stort altare. Istället ville guden göra grekerna skamsna för deras ointresse för matematiken och motvilja mot geometrin.

Oraklet på Delos meddelade atenarna att de skulle bli av med pesten om de konstruerade ett nytt altare, som var dubbelt så stort som det gamla. Anekdoten fick sedan ge namn åt problemet med kubens fördubbling. Pesten som drabbade Aten år 430 f.Kr. hade dock ingen likhet med medeltidens böldpest. Vissa forskare menar istället att atenarna drabbades av tyfus, medan andra hävdar att sjukdomen under de millennier som gått antingen dött ut eller förändrats så mycket att vi inte längre kan känna igen den. Rykande färsk forskning föreslår att det egentligen rörde sig om ett tidigt utbrott av ebola. Notera dock att Platon, som ju är del av anekdoten, år 430 f.Kr. ännu inte var född. Tavlan ovan har målats av den flamländske konstnären Michiel Sweerts.

Det första genombrottet i lösningen av det deliska problemet stod Hippokrates för. Genom en genial upptäckt kunde han reducera problemet till att från två givna linjer, a och b, finna två linjer x och y, sådana att proportionen mellan a och x är densamma som den mellan x och y respektive y och b, eller med modern matematisk notation:

Hur kom då Hippokrates fram till att de två problemen egentligen var ett och samma - att man genom att lösa det ena, också hade löst det andra? Med modern matematik går det relativt enkelt att uttrycka:

Det säger oss att en kub med sidan a, som har volymen a³, förhåller sig till en kub med sidan x, som har volymen x³, på samma sätt som a förhåller sig till b. På så sätt kommer volymen av kuben med sidan a att förhålla sig till kuben med sidan x på samma sätt som linjen a förhåller till linjen b. Uppgiften kan därför förenklas till att från två givna linjer a och x skapa linjerna y och b. Vårt resonemang bygger dock på modern matematik - hur Hippokrates kom fram till samma slutsats får förbli ett mysterium att förbrylla de lärda.

En gång trodde man att man hittat matematikern Archytas skulptur i Villa dei Papyri i Herculeanum nära Pompeji. Senare visade sig statyn istället avbilda Pytagoras. Till villan hörde en gång ett stort bibliotek, som begravdes under askan från vulkanen och på så sätt blivit det enda bevarade antika biblioteket. Mycket av vår kunskap om antiken kommer från de dokument som hittats under utgrävningarna. I romersk tid var villan en samlingsplats för människor som följde den grekiske filosofen Epikuros läror, där filosofiska diskussioner och gott sällskap alltid stod högt i kurs. Foto: Dave Hill och Margie Kleerup, CC-BY-SA 2.0

Det allra största genombrottet vad gäller det deliska problemet kommer dock från en annan antik matematiker, Archytas. Hans upptäckt förbättrades sedan av en annan matematiker, Menaichmos, också han en vän till Platon och dessutom bror till Deinostratos, som löste problemet med cirkelns kvadratur. Archytas lösning är anmärkningsvärd, som Thomas Heath skriver i boken A history of Greek mathematics, "especially when his date is considered (first half of fourth century B.C.), because it is not a construction in a plane, but a bold construction in three dimensions".

Genidraget i Archytas lösning är hans insikt, att skärningspunkten mellan en parabel och en hyperbel skapar en kurva, som vrider sig i tre dimensioner. Med andra ord går den inte att rita ut på ett papper. I Gauss ord är kurvan negativ, men till den tiden skulle det dröja mer än två millennier. En fullständig beskrivning av Archytas lösning kan läsas i Thomas Heaths bok (sid. 246-249), eller i sammandrag på den här hemsidan.

Att den är slående, det är nog det minsta man kan säga om Archytas lösning - det är en komplicerad konstruktion i tre dimensioner, där halvcylindrar och koner trängs med ellipser och cirklar; allt för att konstruera de linjer x och y som Hippokrates anbefallt. Till och med i ett modernt 3D-program är Archytas konstruktion svår att genomskåda - frågan är hur han själv inte bara lyckades föreställa sig en sådan figur, utan även kunde dra slutsatsen att han därigenom hade konstruerat rätt längder.

Hur magnifikt genial Archytas lösning än må vara, kan den inte kringgå den grundläggande svårigheten som gör alla de tre problemen olösliga. Det gäller för π, som i problemet med vinkelns tredelning, och för roten ur π, som i problemet med cirkelns kvadratur, som Pierre Wantzel visade på 1830-talet, men även för kubikroten ur två, som i det deliska problemet. Som den siste store företrädaren för pytagoréernas matematik, måste Archytas ha känt den starkaste frustrationen inför dessa irrationella tal. Problemet är dock inte i sig att talen är irrationella - pentagrammet går trots sina irrationella sidor mycket bra att konstruera geometriskt, något som Euklides visade i sin Elementa. För att konstruera kubikroten ur två krävs däremot en figur i tre dimensioner, vilket var precis vad Archytas levererade. I ett plan, d.v.s. begränsat till två dimensioner, är det - per definition, eftersom kubikroten har just med volym att göra - omöjligt.

Trots det fick alla de tre problemen till slut sin lösning av geniala matematiker och filosofer i Platons generation. Att de fortfarande betraktades som olösliga, beror på att grekerna hade rangordnat de olika lösningsmetodernas elegans. Bäst var de så kallade platonska lösningarna, som skulle genomföras i ett plan med bara passare och omärkt linjal. Därefter kom lösningar med kägelsnitt, som ellipser och parabler. Minst eleganta ansågs de lösningar, där det behövdes ett speciellt verktyg, som Hippias quadratrix-instrument.

Med en vidare definition kan, som grekerna själva visade, alla de tre problemen lösas. Origami är ett annat, kraftfullt alternativ. På sätt och vis var det alltså inte problemen i sig som var omöjliga, utan grekerna själva. Genom Platons idealism, vars popularitet bara skulle stiga, uteslöt de alla möjliga lösningar, och låste sig vid att finna de omöjliga. Samtidigt som de formulerade enkla och eleganta problem, kan man säga, att de i sin jakt på elegans satte på sig sin egen ögonbindel.