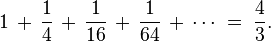Arkimedes - en badare till matematiker

 Trots hårt motstånd, i vilket Arkimedes spelade en avgörande roll, blev Sicilien till slut en självklar och välintegrerad del av det romerska riket. Här ses ruinerna efter den romerska amfiteatern.

Den sicilianske författaren di Lampedusa skrev en gång, att Sicilien var Antikens Amerika, för så många emigranter lockades dit från Grekland av de bördiga flodslätterna, av handeln och av naturresurserna. Många flydde undan politiska förluster, för Greklands politiska system, om än hem åt många tidiga demokratier, var inte barmhärtigt mot sina förlorare; andra flydde undan svält och armod, och ytterligare många flydde undan det persiska rikets expansion in i Jonien, på dagens Turkiets västkust. Många namnkunniga greker följde dessa strömmar västerut, paradoxernas Zenon flyttade till Elea och Pytagoras till Kroton, men Sicilien födde också egna genier, varibland den kanske allra mest berömde var Arkimedes.

Den tankfulle Arkimedes, målad år 1620 av Dominico Fetti, visar antikens stormästare i ingenjörskonst, tillika mästare i matematik och logik, djupt försjunken i tankar.

Vi får föreställa oss Arkimedes värld som den antika grekiska världen stadd i obönhörlig förändring, där de grekiska statsstaterna steg för steg tappade sitt självstyre, krigen gjorde livet hårt för alla, men i synnerhet de små städer, som fick se sin självständighet och sina medborgares liv gjorda till brickor i ett spel mellan större stater och förbund, medan senhellenismens kultur gradvis avlägsnat sig från den klassiska kultur vi vanligen förknippar med det antika Grekland. Sicilien var delvis förskonat det egentliga Greklands öde, men var närmast i konstant krig, antingen inbördes eller placerat, som det var, strategiskt, lukrativt och åtråvärt mitt emellan den gamla sjöstormakten Karthago och det snabbt växande Rom.

Många av Arkimedes texter känner vi från en bönbok från 1200-talet, upptäckt år 1904 av en dansk i Konstantinopel, där man skrapat bort gammalt bläck för att återanvända pergamentet, som på medeltiden var mycket dyrt. Med hjälp av modern teknik har man lyckats läsa vad som stått skrivet i boken innan den barskrapades, så att säga, och flera till av Arkimedes texter fick då se dagens ljus. Texten på palimpesten, som den kallas, förtäljer, bland mycket annat, om en matematisk upptäckt som torde kastat nytt ljus på Zenons paradox, den om Akilles som inte kunde springa ifatt sköldpaddan, liksom kan ses som en tidig viskning om de integraler som inte komma skulle förrän på 1600-talet, ganska så exakt tvåtusen år efter Arkimedes tid.

Arkimedes föreställde sig en parabel, som skurits av av en rät linje, kordan. I den form som bildades, ritade han in en triangel på det sätt som visas i figuren - där triangelns topp befann sig rakt ovanför kordans mitt. Triangelns båda kortsidor, de som inte är den ursprungliga kordan, bildar nya kordor, på vilka satsen kan appliceras på nytt. Om man gör om denna operation oändligt många gånger, torde dessa oändligt många trianglar till slut täcka hela arean, och det går att bestämma förhållandet mellan den första triangelns och hela formens areor.

Om man ansätter att den första triangeln har arean 1, så kommer de två mindre att ha en åttondel av den första areans, eller tillsammans en fjärdedel. Om man bara mäter i horisontalled, det vill säga, längsmed projektionen på x-axeln, så är basen hälften av samma sorts bas hos den första triangeln, eftersom vi konstruerade den så. Genom att använda parabolens egenskaper kunde Arkimedes bestämma att höjden i de små trianglarna är en fjärdedel av den första triangelns höjd, något som blir väsentligt enklare om man använder moderna metoder och sätter in parabeln (som definieras av att de har ekvationer på formen y=ax²+bx+c) i ett koordinatsystem. (Arkimedes egen uträkning, i engelsk översättning, finns på den här sidan. För en härledning på svenska och med moderna matematiska metoder, klicka på bilden längst ned i inlägget.)

Dessa mindre trianglar, som därför har höjden ¼ av grundtriangln och halva bredden, får en åttondel av grundtriangelns area. Eftersom de är två stycken, får andra "generationens" trianglar den sammanlagda arean av ¼ av den förra "generationens" area, eller, med andra ord, om man summerar alla dessa trianglar, börjar man med 1, för den första triangeln, och sedan ¼ för de två i den andra "generationen", och sedan en sextondel för de fyra trianglarna i tredje "generationen", som vardera har arean en sextiofjärdedel. Om man fortsätter i oändlighet får man en serie med oändligt många tal, vardera en fjärdedel av det föregående, och hela parabelns area är täckt.

Detta är vad vi moderna människor skulle kalla en geometrisk summa, och med moderna metoder är det enkelt att använda den geometriska summaformeln, och få reda på att svaret är ¾, d.v.s. att parabolbitens area är fyra tredjedelar så stor som grundtriangelns area, eller vice versa, att grundtriangeln täcker tre fjärdedelar av parabolbiten. Arkimedes, å andra sidan, stred i motvind; dels hade han inte summaformeln att tillgå, och dels trodde många, liksom Zenon, att en oändlig talserie inte kunde ha en ändlig summa.

För att ändå visa, att så var fallet, uppfann Arkimedes en snillrik geometrisk konstruktion, en kvadrat, som han delade i fyra delar. En del av dessa fylldes i för att representera den första fjärdedelen i serien, två lämnade han tomma, och den sista delade han på nytt i fyra delar, där en fylldes i för att representera den andra fjärdedelen i serien, två var tomma, och den sista ytterligare en gång delades, och så fortsatte han. På varje ifylld fjärdedel gick tre tomma, och alltså måste serien en fjärdedel + en sextondel + en sextiofjärdedel och så vidare vara lika med en tredjedel. Eftersom serien började med en etta, för den ursprungliga triangeln, måste svaret vara fyra tredjedelar, och en oändlig serie hade en ändlig summa.

Men det kanske mest användbara av Arkimedes bidrag till matematiken, är hans arbete på att förfina värdet på pi, och att finna en av dess allra bästa användningsområden: formeln för en cirkels area, π r². Arkimedes insåg nämligen, att man kunde skära upp en cirkel på så sätt, att den blev till en rätvinklig triangel, med radien som sin höjd och omkretsen som bas. Genom sina tidigare arbeten, där han bland annat inskrivit cirklar i 96-hörningar och 96-hörningar i cirklar, kände han till formeln för omkretsen,
2π r, och kunde lätt bestämma att arean måste vara (2π r∙r)/2 vilket är lika med just π r².

Den kanske allra mest berömda anekdoten, berättar om hur kung Hieron - som beställt en guldkrona av en juvelerare, men misstänkte att han blivit bedragen - gav Arkimedes i uppgift, att bestämma ifall guldkronan verkligen bestod av solitt guld. Historien förtäljer, såsom som den romerske arkitekten Vitruvius återger den, att Arkimedes låg i badet när han plötsligt fick en snilleblixt, som lärde honom, att ett föremål nedsänkt i vatten tränger undan vatten i förhållande till sin volym, och därefter var det en enkel sak att bara väga kronan och undersöka, om densiteten var den rätta. Simpelt, måhända, men ack så effektivt. Och det lär vara efter den upptäckten han utropade "Heureka!", "Jag har funnit det!", och sprang naken genom Syrakusas gator - för som varje sann antik människa, var det nog på det publika badhuset han badade, och då var det ju klart att han fick bråttom hem för att fortsätta sina experiment.

Arkimedes i badet har blivit en omtyckt symbol för uppfinningsrikedomen, här på ett träsnitt från femtonhundratalet - då publika badhus avskaffats och folk börjat bada i trätunnor istället!

Efter den gamle kung Hierons död, blev Syrakusas politiska lojaliteter mycket mer oklara, och staden verkade byta fot från att stödja romarna, till att ställa sig på Karthagos sida. Rom bestämde sig för att förhindra att staden anslöt sig till ärkefienden, och belägrade år 214 f.Kr. staden under generalen Marcus Claudius Marcellus.

Arkimedes byggde en mängd finurliga konstruktioner, för att jaga iväg romarna, däribland apparater som sköt skurar av småsten genom skottgluggar, en klo som kunde lyfta anfallande skepp och sedan släppa ner dem i havet igen så att de sjönk och en rad brännspeglar för att tända eld på skepp ute till havs, de sistnämnda anses tyvärr mer legendariska än sanna. Det sägs till och med, att de romerska soldaterna blev så rädda, att de flydde var gång de såg en bjälke eller ett rep sticka över stadsmuren, medan Marcellus insåg hur värdefull Arkimedes skulle kunna vara i det krig mot Karthago, som alla visste skulle komma, och gav order om att Arkimedes skulle fångas levande.

En renässanskonstnär vid namn Giulio Parigi tog beskrivningen av skeppsklon som en järnhand högst bokstavligt. Genom åren har många spekulerat i hur Arkimedes gick till väga för att sänka skeppen och kommit fram till flera förslag, både vettiga och fantasifulla, några av vilka finns på denna länk.

Till slut blev dock romarnas belägring för mycket för syrakusanerna, för trots Arkimedes alla sinnrika maskiner kunde inte staden hålla stånd mot det växande romarrikets makt - Siciliens strategiska placering mitt i Medelhavet var alltför åtråvärd. Legenden bjuder, att när romarna bröt in i staden och blodbad utbröt, satt Arkimedes och ritade i sanden, kanske på en ny försvarsmaskin som åter skulle vända krigslyckan, eller på ett nytt banbrytande matematiskt bevis. När han hörde en romersk soldat komma, utropade han "Rubba inte mina cirklar!" Soldaten greps av vredesmod och stack ned den trotsige gamle mannen, utan att först fråga efter hans namn.


Och så, förresten, var det ju den där höjden i den andra triangeln som var en fjärdedel av den första triangelns. Min uträkning till varför det blir så finner du om du klickar på bilden här bredvid.