Medeltida mönster möter modern matematik

I Topkapipalatsets museum ovanför Bosporen förvaras ett oansenligt men hemlighetsfullt medeltida dokument, en nästan 30 meter lång pergamentrulle fylld med geometriska figurer, men utan text. Topkapimanuskriptet andas matematisk historia och medeltida mysterier utan motstycke; dess historia handlar om girihmönster och medeltida mosaik, som tillsammans skulle kunna utgöra material för en matematisk thriller.

Panorama från Topkapipalatset i Istanbul, manuskriptets nuvarande hem, ut över Bosporen.

Men trots att det numer är infogat i Topkapimuséets samlingar som nummer 56, kommer Topkapimanuskriptet inte ifrån Istanbul, utan har sitt ursprung i 1400-talets Persien. Någon författare känner vi inte till, men bakom upptäckten, vars möjligheter manuskriptet torgför, stod med all säkerhet en genialisk matematiker, tillika arkitekt.

Två skisser ur Topkapimanuskriptet som illustrerar  överlagrade mönster, återspeglade eller återspeglingar av en arkitektonisk stil med hela Mellanöstern som spännvidd, och mer därtill. Här finns fler foton ur Topkapimanuskriptet.

Isfahan är inte bara känd för sina gamla broar, som än idag binder samman Zayandeflodens båda stränder, utan även för den mosaik, som bland annat bekläder Darb-i Imamgravens tak. Precisionen, mönstret och effekten som uppvisas hade helt enkelt varit omöjlig utan girihmosaikens metoder - dem som nedtecknades i Topkapimanuskriptet.

Idén bakom girihmönster kan dateras till långt bak i tiden, men någonstans kring 1200-talet skedde en revolution både i exaktheten med vilken mönstren kunde förfärdigas och i komplexiteten hos de mönster som tillverkades. Fram till sekelskiftet mellan 1100- och 1200-talen tror man att alla girihmönster tillverkades med passare och linjal. Eftersom girihmönster bygger på en femfaldig rotationssymmetri, av samma typ som den Dan Shechtman fann i sina kvasikristaller (dem kan du läsa mer om i detta inlägg), blir mönstren aldrig periodiska. Oavsett hur länge man fyller på, kommer mönstret aldrig att se ut precis som det gjorde när man började. Vill man att mönstret skall upprepas, till exempel vara likadant på båda sidor om en portal, får man börja om och göra exakt på samma sätt.

Runt ett valv i den gröna moskén i Bursa, i dagens Turkiet, har en struktur upprepats flera gånger, där varje tiohörning utgör en egen startpunkt, för att skapa ett periodiskt mönster. Mosaiken kan dateras till år 1424.

Ifall man då använder linjal och passare ansamlas småfel, oavsett hur noggrann man är, och det i en sådan takt att allt bortom mycket enkla mönster är otänkbara. De långt mycket mer avancerade mönster man hittar i senare mosaik, som kan innehålla hundratals tiohörningar och ibland upprepas på flera olika längdskalor, blir därför omisskännliga tecken på uppkomsten av en helt ny teknik, byggd på den matematiska insikten, att alla linjer och vinklar kan reduceras ned till fem små, olikformiga mosaikbitar.

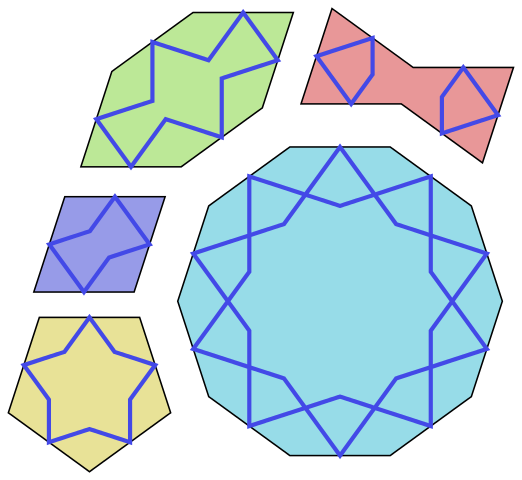Topkapimanuskriptet har givit oss kännedom om de fem girihbitar som de medeltida arkitekterna använde sig av. Bitarna användes som mallar, och när mönstret var färdigt behölls bara de linjer som i figuren målats blå. Här finns en beskrivning av hur man kan bygga egna Girihmönster i gratisprogrammet Google SketchUp.

Den nya metoden spreds som en löpeld och idag kan exempel på girihmönster ses i Indien, Uzbekistan, Turkiet och på många andra platser. Till sin största rätt kom den med de förbättringar som gjordes under 1400-talet, då mönstren blev större, mer komplexa och ibland överlagrade. Det är också vid den här tiden som Topkapimanuskriptet författares. Ett av de bästa exemplen på de mer avancerade mönstren som började dyka upp under 1400-talet hittar man i Darb-i Imamgraven, som färdigställdes år 1453.

På denna mosaik från Darb-i Imamgraven har två mönster överlagrats,  dels ett stort i de svarta linjerna, och dels ett mindre som fyllts i i mellanrummen. Några exempel där tre nivåers mönster överlagrats har man dock inte kunnat finna.

På grund av sina vinklar, som alla är multipler av 36 grader, ger girihbitarna upphov till tio- och femfaldig rotationssymmetri. På så sätt anknyter de till matematiska framsteg som gjorts först under 1900-talet, ett halvt millennium senare.

Peter Lu och Paul Steinhardt, som 2007 publicerade en artikel om girihmönstren, fann nämligen en överraskande likhet mellan de medeltida mönstren och de som Roger Penrose upptäckte år 1974. De upptäckte,  att de fem girihbitarna kan förenklas ytterligare till bara två bitar, Penroses berömda kil och pil, på engelska kallade "kite and dart". (Rapporten i sin helhet kan läsas här.)

Girihmönstren kan förenklas ytterligare till Roger Penroses kil- och pilbitar. Här ses ett exempel på hur tre av bitarna kan konstrueras. De röda och blå strecken till höger i bilden åskådliggör de matchningsregler, som Penrose formulerade och som de medeltida arkitekterna intressant nog ovetandes verkar ha följt. Bilden är från Lu och Steinhardts artikel.

Girihbitarnas släktskap med Penroses mönster gäller inte bara hur de byggs upp, utan de delar också ett antal fundamentala egenskaper. Det betyder inte minst, att de på många sätt innehåller det gyllene snittet. Exempelvis bildar de tiofaldiga symmetriaxlarna som strålar ut från ett girihmönsters centrum tio identiska och likbenta trianglar med vinklarna 36, 72 och 72 grader. Förhållandet mellan den korta och de två långa sidorna i en sådan triangel är det gyllene snittet. Eftersom vinkar på 36 och 72 grader är vanligt förekommande i girihmönstren, blir också gyllene snittet det. Kanske är det också anledningen till att girihmönstren får sitt harmoniska utseende.