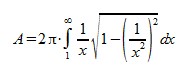Tre geometriska problem

Personligen tycker jag att matematik är som bäst när enkla, okomplicerade frågor leder till avancerade resonemang som till slut blir till lika enkla, eleganta svar. Sådana problem var exempelvis de antika grekerna mästare på att formulera – utan avancerade beräkningsmodeller, numeriska metoder med oändligt många steg eller axiom som strider mot all mänsklig intuition. Tre sådana problem, typiska för den grekiska matematiken, har blivit berömda på grund av sin skenbara enkelhet. Alla skulle lösas med endast passare och onumrerad linjal.

De tre geometriska problemen är alla känneteckna de för den grekiska matematiken, men i många fall är deras exakta uppkomst höljd i historiens dimma. Hippokrates, känd för sina insatser på medicinens område men även som författare till matematiska verk, står bakom en berömd sammanställning av problemen. Här ses ruinerna efter läkekonstens tempel, Asklepieion, på hans hemö Kos. Foto: Wikimediaanvändare Cup of coffee, CC-BY-SA 3.0

1. Vinkelns tredelning eller att dela en vinkel i tre lika delar
Att dela en vinkel i två lika stora vinklar är relativt enkelt, till och med med de sparsmakade verktyg grekerna ställde till vårt förfogande - man kan rent av bevisa att alla vinklar går att dela på mitten med de förutsättningarna. Att dela samma vinkel i tre lika stora delar är desto mer utmanande. Bortsett från ett antal speciella vinklar (3π/2, 9π/4, ja, alla som är en jämn tre-multipel av en konstruerbar vinkel) så krävs för tredelning av en vinkel ett speciellt villkor, som grekerna hade lika svårt för som de hade för siffran noll: Oändligheten.

Vem som först formulerade problemet med vinkelns tredelning är inte känt. Hippokrates, som intresserade sig för de tre problemen, visade däremot att det är möjligt att dela vilken vinkel som helst i tre delar om man har tillgång till en linjal med avståndsmarkeringar. En vinkel CAB kan då med tre steg delas i tre delar:

1. Dra ett streck rakt ned från C, så att det skär linjen AB i punkten D.
2. Fortsätt så att en rektangel bildas, genom att rita till linjerna CF och AF.
3. Rita ett streck AE, så att CHG och CGE blir likbenta trianglar, och HG, GC och GE lika långa som AC. Vinkeln BAG är nu en tredjedel av CAB.

En utförlig beskrivning av Hippokrates lösning på problemet, tillsammans med andra berömda matematikers lösningar, som Arkimedes, Nicomedes och Apollonius, står att finna på den här sidan.

Antagligen var det just eftersom problemet var så lätt att lösa med en numrerad linjal, som det ursprungliga problemet att dela vinkeln med endast en omarkerad linjal sällan fick någon uppmärksamhet. 1837 publicerade fransmannen Pierre Wantzel ett bevis för att det är omöjligt. Även om vissa vinklar går att dela i tre, finns ingen metod som kan dela alla vinklar, så till vida att man inte kan tänka sig att hålla på i all oändlig framtid. Vi som inte vill det får helt enkelt nöja oss med att tredelning är en redigt svår nöt att knäcka.

Problemet med tredjedelar återfinns redan i den mesopotamiska historien om Gilgamesh, som sades vara två tredjedelar gud och en tredjedel människa. Tror man att babylonierna visste om att det krävs oändligt många generationer för att åstadkomma det kan man tolka det som en subtil symbol för, exempelvis, att gudaätten skulle vara oändlig. Tror man inte på den tolkningen, så framstår det som att även de bästa kan göra matematiska felsteg, och att vissa felsteg verkar kunna leva kvar i tusentals år.

2. Cirkelns kvadratur eller att skapa en cirkel med samma area som en kvadrat
Det andra problemet är utan tvivel det äldsta av de tre - intresset för cirkelns area är lika gammalt som civilisationen själv. Svårigheten att från en cirkel skapa en kvadrat med lika stor area är ju ett problem som möter varje person som vill beräkna en cirkels area, eftersom alla areor jämförs i termer av kvadrater (vilket ju är varför vi överhuvudtaget talar om kvadratmetrar).

Den egyptiske skrivaren Ahmes, som står som författare till den berömda Rhindpapyrusen, lär ha givit anvisningen att ta bort en niondel från cirkelns radie och därefter konstruera en kvadrat med den sidan, men den förste som gav sig på att lösa problemet mer exakt var greken Anaxagoras, som enligt den alltid så välinformerade Plutarchos lär ha sysselsatt sig med problemet under tiden han satt i fängelse. Problemet var tydligen populärt bland de antika grekerna, såväl bland matematiker som icke-matematiker - faktum är att det omnämns i den samtida teaterpjäsen Fåglarna av Aristofanes.

Ifall Anaxagoras kom till någon slutsats är inte längre känt. Problemet blev under tiden mycket omtyckt i Grekland, men likväl upptäcktes ingen elegant och enkel lösning på problemet, som bara använde en omärkt linjal och passare. Faktum är att det gick så långt att grekerna började använda beteckningen cirkelkvadrerare för alla dem som utan framgång försöker göra det omöjliga.

Det intressanta med den här tidens lösningar på problemet är att de gick ut på att fylla cirkeln med trianglar eller rektanglar av allt mindre storlek - till slut, tänkte man sig, skulle månghörningen helt fylla cirkeln. Därefter var det lätt att sätta samman dem till en kvadrat och därmed ha löst problemet. Även om metoden fick kritik inte minst från Aristoteles, kan vi i efterhand konstatera att den egentligen var långt före sin tid. Tanken att en area kan beräknas genom att fylla den med oändligt många regelbundna rektanglar och trianglar av allt mindre storlek är inte många steg från 1600-talets integralkalkyl.

En av dem som konstruerade en sådan lösning var filosofen och retorikern Antifon från Aten. Han började med att placera en så stor kvadrat som möjligt i mitten av cirkeln, och fyllde därefter på med allt mindre rätvinkliga trianglar. Metoden återanvändes långt senare av Arkimedes för att ge ett närmevärde till π.

Antifon trodde att [cirkelns] area på detta sätt skulle fyllas, varför vi vid något tillfälle skulle ha en månghörning inskriven i cirkeln, med så små sidor att de skulle sammanfalla med cirkelns omkrets. Och, eftersom vi redan till varje månghörning kan skapa en lika stor kvadrat ... kan vi då också skapa en kvadrat lika stor som en cirkel.” - Simplikios från Kilikien

Staden Elis ligger i en dalgång på Peloponnesos västkust och var hemstaden för Hippias, vars bidrag till matematiken bland annat inkluderade den geniala quadratrix-kurvan med vars hjälp problemet med cirkelns kvadratur nästan kunde lösas. Till staden hörde även antikens Olympia, platsen för de antika olympiska spelen. Här ses den valvförsedda ingången till den antika arenan. Foto: Troy McKaskle, CC-BY-SA 2.0

Det stora genombrottet i lösningen av cirkelns kvadratur kom med matematikern och filosofen Hippias från Elis. Kring år 420 f.Kr. konstruerade han en kurva, som senare har kommit att bli känd som Hippias quadratrix, med vars hjälp han kunde härleda en lösning till problemet med vinkelns tredelning. Någon generation senare visade Deinostratos, en av Platons lärjungar, att den gick att använda även till att lösa problemet med cirkelns kvadratur. Haken med den här metoden var att quadratrixen i sig inte kunde konstrueras med enbart en passare och en omärkt linjal.

För att konstruera Hippias quadratrix behövdes ett särskilt instrument, som bestod av två stavar och en kvadrat. Den ena staven satt fast i kvadratens sidor, på så sätt att den kunde skjutas uppåt och nedåt, medan den andra var fäst i ett av hörnen och med en glidande infästning i den andra staven. Skärningspunkten mellan dem skapade quadratrixen. Bild: Wikimediaanvändar Kmhkmh, CC-BY-SA 3.0

Kan vi med dagens matematik till hjälp lösa problemet med cirkelns kvadratur? För att göra det, behöver vi först betrakta proportionen mellan en kvadrats sida och en cirkels radie. En kvadrat med sidan s har arean s², medan en cirkel med radien r har arean πr². Om vi vill skapa en cirkel med samma area som en kvadrat, får vi först sätta areorna lika, d.v.s.

För att få fram cirkelns radie måste alltså sträckan delas med kvadratroten ur π. Problemet är att roten ur π, liksom π självt, är tal går inte att skapa med de verktyg som grekerna ställde till vårt förfogande. På ett sätt var det just det problemet var det som Arkimedes mötte på, och anledning till att han använde Antifons metod för att skapa en approximation till π. Ytterst beror det på att π är ett s.k. transcendent tal, något som bevisades av matematikern Ferdinand von Lindemann år 1882, vilket i korta ordalag betyder att det inte är en lösning till någon algebraisk ekvation - fast det är en annan historia.

3. Kubens fördubbling eller att bestämma sidan på en kub som är dubbelt så stor som en annan kub
Det tredje problemet är troligtvis det yngsta av de tre problemen. Uppgiften är att att till en kub med känd sida och volym skapa en kub med dubbla volymen. Ganska snart började dock problemet cirkulera i en mer generell form: Att till en given kub konstruera en ny kub, vars volym förhåller sig till den gamla kubens volym med samma proportion som två givna linjers längder förhåller sig till varandra.

Av de tre geometriska problemen var detta det under antiken mest berömda, fast var med anledning av en anekdot om när Aten drabbades av pesten känt som det deliska problemet. Den mest underhållande, men knappast sanningsenliga, versionen av anekdoten ger den hellenistiske matematikern Theon från Smyrna, som återberättar en historia från Eratosthenes numer förlorade verk Platonikos. Han berättar, att när Atens invånarna frågade oraklet på Delos hur de skulle bli av med pesten fick de svaret att de i Apollons, tillfrisknandets gud, tempel skulle konstruera ett nytt altare, som var dubbelt så stort som det gamla. Byggmästarna, vars uppgift ombyggnationen blev, hade ingen aning om hur de skulle gå till väga för att uppfylla gudens önskningar, och rådfrågade därför i sin förvirring Platon. Denne vise herre svarade att guden i själva verket inte alls var intresserad av ett dubbelt så stort altare. Istället ville guden göra grekerna skamsna för deras ointresse för matematiken och motvilja mot geometrin.

Oraklet på Delos meddelade atenarna att de skulle bli av med pesten om de konstruerade ett nytt altare, som var dubbelt så stort som det gamla. Anekdoten fick sedan ge namn åt problemet med kubens fördubbling. Pesten som drabbade Aten år 430 f.Kr. hade dock ingen likhet med medeltidens böldpest. Vissa forskare menar istället att atenarna drabbades av tyfus, medan andra hävdar att sjukdomen under de millennier som gått antingen dött ut eller förändrats så mycket att vi inte längre kan känna igen den. Rykande färsk forskning föreslår att det egentligen rörde sig om ett tidigt utbrott av ebola. Notera dock att Platon, som ju är del av anekdoten, år 430 f.Kr. ännu inte var född. Tavlan ovan har målats av den flamländske konstnären Michiel Sweerts.

Det första genombrottet i lösningen av det deliska problemet stod Hippokrates för. Genom en genial upptäckt kunde han reducera problemet till att från två givna linjer, a och b, finna två linjer x och y, sådana att proportionen mellan a och x är densamma som den mellan x och y respektive y och b, eller med modern matematisk notation:

Hur kom då Hippokrates fram till att de två problemen egentligen var ett och samma - att man genom att lösa det ena, också hade löst det andra? Med modern matematik går det relativt enkelt att uttrycka:

Det säger oss att en kub med sidan a, som har volymen a³, förhåller sig till en kub med sidan x, som har volymen x³, på samma sätt som a förhåller sig till b. På så sätt kommer volymen av kuben med sidan a att förhålla sig till kuben med sidan x på samma sätt som linjen a förhåller till linjen b. Uppgiften kan därför förenklas till att från två givna linjer a och x skapa linjerna y och b. Vårt resonemang bygger dock på modern matematik - hur Hippokrates kom fram till samma slutsats får förbli ett mysterium att förbrylla de lärda.

En gång trodde man att man hittat matematikern Archytas skulptur i Villa dei Papyri i Herculeanum nära Pompeji. Senare visade sig statyn istället avbilda Pytagoras. Till villan hörde en gång ett stort bibliotek, som begravdes under askan från vulkanen och på så sätt blivit det enda bevarade antika biblioteket. Mycket av vår kunskap om antiken kommer från de dokument som hittats under utgrävningarna. I romersk tid var villan en samlingsplats för människor som följde den grekiske filosofen Epikuros läror, där filosofiska diskussioner och gott sällskap alltid stod högt i kurs. Foto: Dave Hill och Margie Kleerup, CC-BY-SA 2.0

Det allra största genombrottet vad gäller det deliska problemet kommer dock från en annan antik matematiker, Archytas. Hans upptäckt förbättrades sedan av en annan matematiker, Menaichmos, också han en vän till Platon och dessutom bror till Deinostratos, som löste problemet med cirkelns kvadratur. Archytas lösning är anmärkningsvärd, som Thomas Heath skriver i boken A history of Greek mathematics, "especially when his date is considered (first half of fourth century B.C.), because it is not a construction in a plane, but a bold construction in three dimensions".

Genidraget i Archytas lösning är hans insikt, att skärningspunkten mellan en parabel och en hyperbel skapar en kurva, som vrider sig i tre dimensioner. Med andra ord går den inte att rita ut på ett papper. I Gauss ord är kurvan negativ, men till den tiden skulle det dröja mer än två millennier. En fullständig beskrivning av Archytas lösning kan läsas i Thomas Heaths bok (sid. 246-249), eller i sammandrag på den här hemsidan.

Att den är slående, det är nog det minsta man kan säga om Archytas lösning - det är en komplicerad konstruktion i tre dimensioner, där halvcylindrar och koner trängs med ellipser och cirklar; allt för att konstruera de linjer x och y som Hippokrates anbefallt. Till och med i ett modernt 3D-program är Archytas konstruktion svår att genomskåda - frågan är hur han själv inte bara lyckades föreställa sig en sådan figur, utan även kunde dra slutsatsen att han därigenom hade konstruerat rätt längder.

Hur magnifikt genial Archytas lösning än må vara, kan den inte kringgå den grundläggande svårigheten som gör alla de tre problemen olösliga. Det gäller för π, som i problemet med vinkelns tredelning, och för roten ur π, som i problemet med cirkelns kvadratur, som Pierre Wantzel visade på 1830-talet, men även för kubikroten ur två, som i det deliska problemet. Som den siste store företrädaren för pytagoréernas matematik, måste Archytas ha känt den starkaste frustrationen inför dessa irrationella tal. Problemet är dock inte i sig att talen är irrationella - pentagrammet går trots sina irrationella sidor mycket bra att konstruera geometriskt, något som Euklides visade i sin Elementa. För att konstruera kubikroten ur två krävs däremot en figur i tre dimensioner, vilket var precis vad Archytas levererade. I ett plan, d.v.s. begränsat till två dimensioner, är det - per definition, eftersom kubikroten har just med volym att göra - omöjligt.

Trots det fick alla de tre problemen till slut sin lösning av geniala matematiker och filosofer i Platons generation. Att de fortfarande betraktades som olösliga, beror på att grekerna hade rangordnat de olika lösningsmetodernas elegans. Bäst var de så kallade platonska lösningarna, som skulle genomföras i ett plan med bara passare och omärkt linjal. Därefter kom lösningar med kägelsnitt, som ellipser och parabler. Minst eleganta ansågs de lösningar, där det behövdes ett speciellt verktyg, som Hippias quadratrix-instrument.

Med en vidare definition kan, som grekerna själva visade, alla de tre problemen lösas. Origami är ett annat, kraftfullt alternativ. På sätt och vis var det alltså inte problemen i sig som var omöjliga, utan grekerna själva. Genom Platons idealism, vars popularitet bara skulle stiga, uteslöt de alla möjliga lösningar, och låste sig vid att finna de omöjliga. Samtidigt som de formulerade enkla och eleganta problem, kan man säga, att de i sin jakt på elegans satte på sig sin egen ögonbindel.

Historien om två målare som skulle måla en trumpet

Först tänkte jag återberätta vad som kan kallas en "matematisk rolig historia", eller åtminstone en paradox.

Om man tar kurvan till y=(1/x), vilket är ett mycket vanligt exempel på en asymptot (dvs. en kurva som närmar sig en linje utan att någonsin nå den, i det här fallet linjerna x=0 och y=0), och ritar upp den för x>1 så blir resultatet en backe som börjar i y=1 då x=1 och får y=0 då x når oändligheten.

Roteras denna kurva kring x-axeln, så att en rotationskropp skapas, blir resultatet en oändligt lång trumpet. Men eftersom matematikens natur så är denna kurva färglös sätter vi två målare på att måla den i en dyr djupblå kulör. De får vardera en burk färg, och måste måla hela kurvan, ända bort till oändligheten. Om den ena får i uppdrag att måla kurvan med pensel, medan den andra får i uppdrag att fylla kurvan med blå färg - vem förbrukar mest av den dyra färgen?

Det självklara och intuitiva svaret på den här frågan är naturligtvis den som fyller kurvan (det måste väl gå åt mer om man fyller kurvan än om man bara målar dess sidor?) - trots att jag redan från början skrev att det var en paradox. Det rätta svaret är därför att den som målar med pensel förbrukar mest färg.

Att måla trumpeten betyder att målaren måste gå längsmed hela kurvan, och måla varje halvmeter med penseln för sig. Oavsett hur snål och sparsam målaren är med färgen, kommer förbrukningen att vara i evigt, eftersom kurvan är oändligt lång. Den som skulle fylla kurvan å andra sidan behöver bara stå på ena sidan, och eftersom arean under en 1/x-kurva är möjlig att bestämma matematiskt, det vill säga att den är begränsad och har ett värde, kan vi avgöra hur mycket färg den här målaren kommer att förbruka.

Formeln för längden av en kurva är

eller mer specifikt för vårt fall (nu multiplicerad med radien 1/x och 2 π eftersom det är arean av kurvan vi vill åt)

Denna integral går mot oändligheten, varför målaren som målar med pensel aldrig kommer att bli klar. "Volymen" på "trumpeten" bestäms av en vanlig integral insatt i formeln för en cylinders volym (eftersom trumpeten i grund och botten är en mycket uttänjd och ihopdragen cylinder, där höjden har ersatts med en annan, icke-horisontell funktion) och målaren som fyller trumpeten kommer att bli klar ganska snart. Volymen är nämligen begränsad enligt

hur otroligt det än må låta. (Enheten här är volymenheter, men beror av vad som ansätts på axlarna.)

Formeln som jag använde för att bestämma kurvans längd är egentligen höjdpunkten (inte ens jag märkte det) i dagens inlägg. Den härleds genom att man väljer ett litet delta-x (jag tänker inte ge mig på att skriva den grekiska bokstaven delta här och nu) och får därför ett delta-y. Om man använder Pythagoras sats på dessa får man en delta-längd på kurvan uttryckt i x och/eller y. Med lite förenkling och integration har man formeln. Detsamma gäller ifall man önskar den för ett polärt koordinatsystem.

Den formeln är ett ganska så kraftfullt verktyg, även om den innehåller en kvadratrot som gör den svår att lösa exakt. I fall som dessa gör sig därför numeriska integraler ganska väl.

Det gyllene snittet under fem tusen år

Hunden, människans bäste vän? Inte då, det gyllene snittet låter sig inte besegras så lätt! "De lyckliga hundarna" av Richard Ansdell.

Alltsedan de kambriska havens värld har det funnits snäckor, anfäderna till dagens snäckor, de snäckor vars skal urmänniskorna plockade och beundrade längs stenålderns havsstränder, och de besitter en matematisk hemlighet. Fast deras koppling till det gyllene snittet är nog inte så vidare hemlig längre. Fortfarande, efter att ha levt i en värld där vi ser det gyllene snittet varthän vi än vänder våra ögon, verkar det aldrig upphöra att fascinera oss. Kanske är det just därför vi dras till det, kanske är det vår världs emblem. Och mer exakt är talet ett plus kvadratroten ur fem genom två, eller det gyllene snittet.

Att både snäckor och kottar, lika väl som solrosor och myriader av andra ting i naturens värld går att hänföra till det gyllene snittet var kanske just den inspirationskälla som ligger till grund för den konst och matematik som följt i dess spår. Både som proportion, det gyllene snittet, och som sidorna på en rektangel, den gyllene rektangeln, har talet följt med oss sedan urminnes tider. Rektangeln lär vara den skönaste möjliga, utvald av människor i alla kulturer. Och då måste den vara ett framgångsrecept för den som vill skapa slående konst.
Somliga tror att redan de gamla egyptierna kom underfund med detta i sitt sökande efter en byggnad som kunde överskrida barriären till livet efter detta - den som ställer sig mitt på en av pyramidernas sidor, förväntas komma fram till att avståndet till toppen, längs med ytan, förhåller sig med det gyllene snittet till tre decimalers noggrannhet till avståndet till pyramidens centrum. För den äldsta befästa användningen av det gyllene snittet får vi dock vänta ytterligare ett och ett halvt millennium, till det antika Grekland.

Gyllene snittet eller inte, ligger pyramidernas skönhet i deras matematik?

Man kan säga, att den grekiska matematiska traditionen sträcker sig från Thales från Miletos, via hans lärjunge Pythagoras och Pythagoras lärjungar tills Sokrates, Platon och Aristoteles. Däremellan finner vi Euklides, och, runt den tid då Parthenon på Akropolis i Aten uppfördes, skulptören Fidias. Fidias betraktades redan av romarna som en av Greklands mest briljanta konstnärer, med både ett av den antika världens sju underverk bland sina skapelser och de två statyerna av Athena, staden Atens skyddsgudinna, som då prydde templet, och deltog i att göra det världsberömt. Hans verk lever idag endast genom kopior, varav de flesta gjordes under romersk tid, men minnet av honom har idag fått en återfödelse genom att man under 1900-talet lät den första bokstaven i hans namn, den grekiska bokstaven φ, fi, beteckna den proportion som var pionjär med att använda. Det gyllene snittet skrivs därför ofta

Pythagoréerna höll det gyllene snittet som en gudomlighet i sin av talmystik uppbyggda världsbild, liksom π, men blev av båda djupt besvikna, när det upptäcktes att de var irrationella, och således gick på kors med en annan av pythagoréernas grundprinciper, att alla tal kan skapas genom att dela två heltal med varandra. Den uppfattningen fanns för övrigt i stort i hela det antika grekiska samhället, och det var därför inte så märkligt att grekerna vände sig till bråken när de försökte uttrycka tal som pi eller det gyllene snittet i siffror. Idag brukar vi ju benämna dem approximationer, men jag skulle kunna tänka mig att de antika grekerna i alla fall för en stund trodde sig ha funnit det exakta uttrycket. Likaväl kan man ju föreställa sig den antike grekiske matematiker som med ljus och lykta söker längsmed tallinjen av idel rationella tal; "Men det måste ju finnas någonstans här!". Men lika besvikna över det gyllene snittet som över pi behövde pythagoréerna inte bli; ett vanligt sätt att definiera det gyllene snittet på är faktiskt med hjälp av ett bråk:

där förhållandet a till b motsvarar det gyllene snittet, vilket man ser om man sätter in b=1, eftersom man då får a=φ; sätter man in b=2 får man a=2φ. Om man då just sätter in b=1 så får man istället en andragradsekvation, vars lösning är just det gyllene snittet:

Den visar på en av det gyllene snittets kännetecknande egenskaper, nämligen att φ i kvadrat är detsamma som φ+1. (Något man får fram om man adderar x+1 till vardera sidan.)

Ett fragment från en avskrift av Euklides Elementa från omkring 100 e.Kr., det matematiska grundverk som också innehåller den första matematiska beskrivningen av det gyllene snittet.

Den första matematiska beskrivningen av det gyllene snittet står dock att finna i Euklides Elementa, ett av matematikens absoluta grundverk. Euklides, utöver att han bland annat visade att det gyllene snittet är irrationellt, gav den kanske enklast möjliga geometriska definitionen av det gyllene snittet, den som inspirerade det matematiska uttryck som vi använde som startpunkt precis här ovanför. Euklides, som kallar proportionen för den ytterlighetens och medelvärdets förhållande, i fri översättning från engelskan, eftersom min antika grekiska tyvärr är i behov av allvarligt förbättringsarbete, definierar den genom att dra en rät linje och dela den i två, så att en kort och en lång del skapas. Han säger då att den korta förhåller sig till den långa biten med det gyllene snittet, ifall det råder samma proportion mellan dem, som det gör mellan den långa biten och hela sträckan. Rent och elegant, men i behov av en illustration:

Euklides definition av det gyllene snittet; där proportionen mellan a och b är densamma som proportionen mellan a och hela sträckan, a+b. Definitionen är fortfarande, med över två millennier på nacken, en av de mest använda.

Det skulle dock dröja mer än tolv hundra år innan en man upptäckte vidden av det gyllene snittets nära koppling till talens självaste natur; hans namn var Fibonacci. Boken han lät publicera år 1202 var banbrytande på många sätt (se detta inlägg), inte minst för den studie på kaniner han beskrev. Varje kanin, enligt Fibonacci, föder en ny kaninunge per månad, som tar en månad att växa upp innan den skaffar egna kaninungar. Onödiga komplikationer som att det måste vara två kaniner för att det överhuvudtaget skall bli kaniner skalade Fibonacci bort. En kaninunge kommer därför inte att skaffa någon kanin månad ett. Månad två gör den dock så, och då finns det två kaniner. Men den nyfödda kaninen är för ung, och nästa månad föds det fortfarande bara en kanin, och det finns tre kaniner. Men då finns det med en gång två kaniner som skaffar kaninungar, och nästa månad finns det fem kaniner, tre vuxna och två ungar. Följaktligen finns det månaden därpå fem kaniner, sedan åtta, tretton, tjugoett och trettiofyra. Fibonaccis talserie är skapad.

Men det förbluffande är fortfarande kvar; om man delar ett fibonaccital, som vi kallar F(n), med fibonaccitalet innan, F(n-1), får man, ju större fibonaccital man väljer, en kvot allt närmare phi, det gyllene snittet. Vi kan se att 2/1=2; 3/2=1,5; 5/3=1,66...; 8/5=1,6; 13/8=1,625; 1,61538...; och så vidare; 39088169/24157817=1,618033989... om x är kvoten mellan ett fibonaccital och det förra, så får vi

Beviset var dock inte Fibonaccis förtjänst, utan utformades av Johannes Kepler, ett århundrade senare. Ungefär samtidigt publicerades den första decimalapproximationen av det gyllene snittet, av Michael Maestlin, år 1597, istället för de bråk som grekerna försökte fånga det gyllene snittet i, och som Euklides visade var omöjligt, ändock är det lika omöjligt att skriva talet som ett decimaltal.

Under upplysningen fann man många exempel på det gyllene snittet i naturen, som gick väl i linje med tidens melodi: att världen är matematisk som ett klockverk. 1835 benämndes proportionen för första gången det gyllene snittet, istället för Euklides ytterlighetens och medelvärdets förhållande, och på nittonhundratalet fick Fidias ge namn åt förhållandet. Men det gyllene snittet ligger alltför nära vår värld för att försvinna med den deterministiska, förutsägbara och urverkslika världsbilden, och dyker upp till och med i Roger Penrose mönster och Dan Shechtmans Nobelprisbelönade kvasikristaller. Men det är en annan historia.

Är det gyllene snittet med och leder oss in i en fjärde rumsdimension? En legering av zink, mangan och holmium uppvisar ett oregelbundet mönster med det gyllene snittets proportioner. Bild: Wikimedia Commons-användare Materialscientist, CC BY-SA 3.0

För exempel på det gyllene snittets förekomst i geometrin, se den här externa sidan.

Ägg, påskharar och matematiska beräkningar

Nu närmar sig påsken med stormsteg och förhoppningsvis har värmen kommit för att stanna. Påsken infaller som bekant efter vårdagjämningen – det dygn då dag och natt är lika långa – nämligen, enligt tumregeln, den första söndagen efter den första fullmånen efter vårdagjämningen.

Påsken är en av kyrkoårets viktigaste högtider, och bristen på en gemensam dag att fira den på utgjorde ett problem för den tidiga kyrkans sammanhållning. Firandet har dock fått olika tema i olika länder, som denna bild från Santiago de Compostela. Foto: J. Pereira, CC-BY-SA 2.5

Men det var som sagt bara tumregeln. Verkligheten är som vanligt långt mycket mer komplicerad, och de munkar som under medeltiden hade för uppgift att beräkna påskens datum var ofta i den dåtida framkanten av matematiken. Beväpnade med Ptolemaios (ca 90-168 e.Kr) bild av solsystemet, med epicykler och jorden i centrum (se äldre inlägg här och här om denne briljante men ack så misstagne matematiker och astronom) och antik grekisk, medeltida bysantinsk, arabisk och europeisk matematik arbetade de fram tabeller över påskens datum långt in i framtiden.

Diskussioner om när påsken skulle infalla har förts åtminstone sedan mötet mellan påven Anicetus och biskopen Polykarpos av Smyrna år 154 e.Kr., men det var först vid det första konciliet i Nicaea (som idag ligger på Turkiets västkust) år 325 som den kristna världen fick ett gemensamt sätt att beräkna påsk. Då beslutades att hela kristendomen skulle använda det sätt som var bruk i Alexandria. Det tog dock flera århundraden innan hela den kristna världen accepterat bestämmelsen.

Denna illustration från 1493 av konciliet i Nicaea återfinns i den berömda Nürnbergkrönikan, som skildrar den kristna världens historia. Konciliet i Nicaea sammankallades av den kristne romerske kejsaren Konstantin, bland annat för att fastlägga påskens datum.

Det system som då infördes används fortfarande idag, fast på lite olika sätt. Först och främst delas året in efter en månkalender – året får tolv månader, på vardera vanligen 29 dagar – men ett sådant år är elva dagar för kort. Varje år kommer månkalendern alltså elva dagar till efter solkalendern. (Mån-månaderna definieras på så sätt att fullmånen – den formella fullmånen, som inte nödvändigtvis överensstämmer med verklighetens fullmåne – inträffar på månadens fjortonde dag.) När tre år gått och månkalendern ligger 11·3 = 33 dagar efter, skjuts en extra månad in på 30 dagar. De överskjutande dagarna blir alltså 33-30 = 3. Nästa år blir de elva till, året därpå och året därpå igen också, tills de överskjutande dagarnas antal når 3+3·11 = 36. En extra månad läggs till och, ja, dagarna minskas till 6. På det här viset upprepas processen tills de överskjutande dagarna är -1, d.v.s. tills månkalendern ligger en dag före solkalendern, något som inträffar på det nittonde året. Då läggs en skottdag in – då månen formellt sett står stilla – och kalendern börjar om. Därför går månkalendern i cykler om nitton år.

Den första månad i vilken den fjortonde dagen (dess formella fullmåne) i denna månad hamnar på eller efter vårdagjämningen den 21 mars är påskmånaden och den första söndagen efter den fjortonde dagen i denna månad är då påsken infaller. Påsken infaller som tidigast om den fjortonde dagen i någon mån-månad är just den 21 mars, samt detta är en lördag. Söndagen som följer därpå måste alltså bli påsk, som således inträffar den 22 mars. Om å andra sidan påsken inträffar den femtonde i denna månad väntar påskmånaden till nästa månad, och dess fjortonde dag blir då den 18 april. Om denna dag vidare själv skulle vara en söndag, väntar påsken till nästa söndag, som blir den 25 april, vilket är det senaste datum påsken kan inträffa.

Eftersom vårdagjämningens datum (satt i solkalendern), månens formella fullmåne (fixerat till den fjortonde i varje månad i månkalendern) och veckodagarna här samvarierar, hoppar påsken fram och tillbaka i en cykel på nästan 6 miljoner år. Sannolikheten att påsken skall inträffa ett visst datum framgår av diagrammet. Är man osäker och skall gissa, förefaller stalltipsen vara den 19 april (och det med en hisnande säkerhet på nära fyra procent).