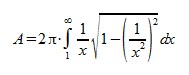Ett litet cirkelresonemang

Det är lätt att förledas tro att städer är organiska. Det räcker att se hur stor del som består av trä – och inte att glömma, människor; de är ju själva kärnan i varje stad. Även om man skulle kunna resonera att trähusstäder likaväl som stenhusstäder (i viktprocent) huvudsakligen består av sten och grus, så var det inte det jag menade.

Det är även lätt att förledas tro att städer växer enligt organiska mönster – eller, det vill säga, i organisk avsaknad av mönster –  att de breder ut sig av sig själva, sväljer böljande kullar, dämmer ut marskland och leder om floder, och att de gör så organiskt, utan planering.

Den världsberömda toskanska staden San Gimignano, skiss av Joseph Pennel, 1883

Den känsla (det är inte för inte människor nästintill vallfärdar till San Gimignano) som finns i en sådan, organisk, stad är något som många stadsplanerare försökt återskapa. Det är någonting i de vindlande gatorna som fångar och som trollbinder; inte bara det att de skyddar mycket bättre mot vind och kyla än de långa, breda avenyer som sedermera har blivit – och fortfarande är – moderna. Själv skulle jag förmoda, att ett mer detaljrikt arkitektoniskt formspråk är mindre känsligt mot att någon detalj försvinner eller förfars – om mönstret inte är uppenbart, blir det inte märkbart mindre uppenbart om en del av det uteblir – medan om man istället har en minimalistisk stadsplanering ser allting fantastiskt ut i datormodellen där det är helt och rent, men så blir det tyvärr aldrig i vår allestädes närvarande verklighet.

Men allt det där var ett stickspår, och ett alldeles för långt sådant också om man sätter den sidan till, för huvudnyheten är en nyhet som mer sanningsenligt skulle benämnas gammelhet numera, presenterad i denna artikel i SvD. Där presenteras nämligen teorin om att alla dessa fina, charmiga organiska städer inte överhuvudtaget var organiska, utan snarare frukten av mästerlig och rationell stadsplanering.

Medeltidens stadsplanerare var inte ensamma om att uppskatta cirkelformade gator, Royal Crescent i Bath, är ett exempel på det georgianska Englands arkitektur, även om just den här gatan nog inte får lä av sin cirkelform. En bit bort syns ytterligare en cirkelformad gata, The Circus.

Snarare, menar man, att vår uppfattning om den "organiska", medeltida staden är en nostalgisk missuppfattning, född ur jämförelsen av industrialismens rektangulära Manhattan och de raka gatorna i de romerska garnisonsstäderna med mysiga, ofta kulturminnesmärkta städer från 1000-talets våg av stadsgrundanden. Istället menar Klaus Humpert och Martin Schenk som skrivit den bok artikeln refererar, Entdeckung der mittelalterlichen Stadtplanung, eller ungefär "Upptäckten av medeltidens stadsplanering", att städerna ritades upp efter detaljerade stadsplaner bestående av regelbundna geometriska former: rektanglar, cirklar, trianglar, kvadrater och oktagoner.

Definitionen av en cirkel (var vänlig och plocka fram den högdragna rösten) är att alla punkter längsmed dess omkrets har samma avstånd till en och samma fixerade punkt i planet. Och det ger den en rad spännande egenskaper. För det första har den oändligt många hörn, vilket innebär att den ger mesta möjliga area med minsta möjliga omkrets. För det andra ger den ett behov, och en möjlighet, att bestämma π. Man skulle visserligen kunna finna rader av spännande egenskaper, men just denna leder oss in på något annat spännande – nämligen ytterligare en antik grekisk hatkärlek: Cirkeln och Sfären.

I den grekiska världsbilden, kom dessas perfektion näst efter det gyllene snittet (länk till tidigare inlägg); Aristoteles ansåg att hela universum var uppbyggt av en rad överlagrade sfärer med jorden i mitten, en vy senare övertagen av kyrkan; de antika grekerna var långt ifrån främmande från idén att jorden i sig skulle vara en sfär och Ptolemaios (och i synnerhet det efterföljande millenniets astronomer) gick långt i sina försök att bevisa att alla planeterna rörde sig i cirklar och cirklar på andra cirklar, cykler och epicykler, runt jorden. Den åsikten, bortsett från solens och epicyklernas plats respektive varande i det hela, hade för övrigt även Kopernikus. Pythagoréerna (länk till tidigare inlägg) lär dessutom har sett cirkeln som en symbol för själen.

Även om det ptolemeiska systemet fortsätter att ge nästan lika noggranna förutsägelser om planeternas plats på himlen, är dess komplexitet hisnande. Den spanske kungen Alfonso X, som försökte reda ut problemet, lär i desperation när planeterna fick över 40 epicykler var ha utropat att han om ha varit med vid skapelsen, så hade han kunnat ge några goda råd.

Men, liksom alltid och liksom med det gyllene snittet, fanns det en lite hake. De antika grekerna var nämligen av den åsikten, att alla tal skulle gå att uttrycka i bråkform, vilket, förargligt nog, inte är möjligt med varken φ, det gyllene snittet, eller π – även om många genom årens lopp har försökt; vissa har faktiskt kommit mycket nära. Till råga på allt är π transcendentalt, det vill säga är inte roten till någon algebraisk ekvation.

Cirkeln som konstnärlig form har uppskattats i många kulturer, kanske för att den, till skillnad från vår egen värld, har ett så klart centrum. Detta silkesföremål i mongolisk stil stammar från det medeltida Mesopotamien och är 79 cm i diameter.

Cirkeln återkommer genom vår kulturhistoria. Leonardo da Vincis vitruvianske man är ett exempel, andra är alla de cykliska förlopp som ständigt omger oss, liksom det berömda ekorrhjulet. Faktum är att de är så vanliga att det är lätt att förledas tro att allt är cykliska förlopp, för att, så att säga, sluta cirkeln.

Och slutligen vid närmare eftertanke: Om något inlägg, så kan detta omöjligtvis ha varit ett stickspår. Anledningen är enkel: jag har aldrig sett ett cirkelformigt sådant. För vändplatser räknas väl inte?

Mätning, meter och mäteri – meterns historia

Även om vår måttskala för temperatur – den som är 0 grader vid vattnets fryspunkt och 100 vid dess kokpunkt och uppkallats efter sin uppfinnare, Anders Celsius – är en svensk uppfinning rimmar den mycket likt de nya måttskalor som skapades under den franska revolutionen. Ett sätt att se revolutionen 1789 är som ett uttryck för en vilja att ändra, att effektivisera och att modernisera, där jämlikhet och modernisering skulle gå hand i hand med förenkling och standardisering, inte minst av måttsystemen. De nya måttenheterna skulle vara frikopplade från historiska orsaker, religion och rivaliteter.

Reformivern under sjuttonhundratalets slut tog sitt uttryck inte bara inom politiken, utan även inom naturvetenskaperna. Med samma dramatik som Robespierre lät halshugga den gamla regimens företrädare, som på den här anonyma 1800-talstavlan avbildats strax före gripandet, for de revolutionära matematikerna, fysikerna och kemisterna ut mot de gamla och förlegade måttenheterna.

Det nya systemets förlänades tack vare sin överskådlighet och sammanhållning för det mesta framgång, även om de radikala förändringarna mötte på visst motstånd, inte minst från dem som hellre ville se en omarbetning av det gamla systemet. Revolutionärernas reformiver stammade visserligen ur ett starkt behov, men grundade sig inte enbart på en vilja att effektivisera, utan även hade även en ideologisk dimension. Den religiöst betingade sjudagarsveckan skulle exempelvis ersättas med en tiodagarsvecka, där varje dag skulle bestå av tio timmar, varje timma av hundra minuter, och så vidare. Det behöver knappast sägas att just den delen av reformerna inte blev särdeles långlivad.

Behovet av ett nytt och sammanhållet måttsystem för vetenskapligt bruk var vida erkänt och på de flesta andra områden rönte revolutionärerna väsentligt större framgång, inte minst på längden och på vikten. De gamla foten och alnarna och alla andra längdmått av varierande omfång ersattes av metern och från den avleddes en rik uppsättning av helt nya, decimala enheter med logiska benämningar: kilometern, centimetern, litern (en kub med sidan en tiondels meter), grammet (vikten av en tusendels liter vatten) och kilogrammet, bara för att nämna några.

Jean-Charles Borda var vid den här tiden en av Frankrikes mest framträdande matematiker och vetenskapsmän, som sedermera fick i uppdrag att leda arbetet med att definiera meter. Känd är han även för sitt arbete med logaritmer, och på den här bilden syns han i färd med att utföra mätningar på Teneriffa.

Inte bara vetenskapen, utan hela den europeiska världsbilden var under snabb förändring. Fenomen som tidigare varit mystiska fick naturvetenskapliga förklaringar, samtidigt som handeln utvecklades och gjorde att lokala måttsystem blev alltmer opraktiska. Nydefinitionen och standardiseringen av Europas måttsystem hänger således tätt samman med upplysningens vetenskapliga framsteg såväl som med ekonomins förändring, i en process som började redan under sextonhundratalet och löpte genom hela sjuttonhundratalet.

Införandet av de nya måttenheterna gick på många sätt hand i hand med en stark vetenskaplig utveckling. Uppfinnandet av nya, precisare instrument gjorde exakta måttenheter nödvändiga, måttenheter som tidigare hade varit stort sett meningslösa utan de exakta instrumenten att mäta upp dem med. På samma sätt gjorde de nya instrumenten klart att världen verkligen var mätbar, att den kunde sammanfattas med siffror och mått och att matematiken med måttenheternas hjälp kunde användas för att undersöka och utforska den.

De vetenskapliga framstegen tydliggjorde att matematiken var ett användbart verktyg för att avbilda världen, men visade också på behovet av måttenheter. Ett ensamt tal säger inget om verkligheten, för det krävs en måttenhet. Måttenheten är själva bandet mellan matematiken och dess omvärld, som gör det möjligt att med matematikens hjälp beskriva verkligheten. För att uppfylla sitt syfte måste måttenheten därför vara exakt och universell, och helst stämma med överens med den europeiska matematikens sedan länge inarbetade tiobas.

En fransk lieue motsvarade exempelvis ca 3,3 kilometer i Beauce och 5,8 i Provence, och en Ruthe i Bern motsvarade 2,9 moderna metrar, medan den i Basel motsvarade 4,9. Det finns än mer hårresande exempel – en timmas resa, på tyska Wegstunde, betydde 3,71 kilometer i Tyskland medan schweizarna trots alla sina berg kom nästan en kilometer längre, nämligen 4,8 kilometer. Om resan tillgick på det sätt som David Cox har avbildat den, blir man plötsligt varse svårigheterna i att mäta avstånd.

De måttenheter som tidigare funnits i Europa var inte exakta, i synnerhet inte enhetliga och hade för det mesta en kombination av tolv- och tjugobas – på samma sätt som det engelska pundet fram till 1971 bestod av 20 shilling som vardera motsvarade 12 pence. Systemets icke-decimala natur var i mångt och mycket ett arv från det romerska måttsystemet, där en libra, en viktenhet som i moderna mått motsvarade ett tredjedels kilo, delades upp i tolv unciae, en uppbyggnad som passade bra för att göra det lätt att skapa många olika bråkdelar och kombinationer. (I det här inlägget kan du läsa mer om Europas gamla måttenheter.)

Redan tidigt hade röster för ett enhetligt, vetenskapligt och helst decimalt måttsystem höjts, bland annat i en skrift från 1668 av den engelske prästen och naturfilosofen John Wilkins. Wilkins föreslog att man skulle definiera en längdenhet, eller universellt mått som han själv benämnde det, som sträckan mellan ändpunkterna hos en sekundpendel, d.v.s. en pendel som går från ena sidan till den andra på exakt en sekund. Sju år senare gav det italienske universalgeniet Tito Livio Burattini mer eller mindre ovetandes metern dess namn, när han översatte Wilkins beteckning till italienska.

John Wilkins ville skapa en universell enhet, definierad som längden. Sedan början av 1600-talet var det känt att pendelns periodtid, d.v.s. tiden det tog för den att svänga fram och tillbaka en gång, endast berodde av pendelns längd. En pendel med en definierad periodtid, i det här fallet två sekunder, kunde därför användas för att definiera ett avstånd. Närmare bestämt gav den meterns längd som 99,4 cm.

Den franske astronomen Jean Richer, som på uppdrag av den franska vetenskapsakademin befann sig i Cayenne, i Franska Guyana på Sydamerikas nordkust, blev den som upptäckte problemet med Wilkins definition. Han upptäckte, utöver sina astronomiska observationer, att pendelavståndet hos en sådan sekundpendel var en tredjedels centimeter kortare i Cayenne än i Frankrike, och inte alls så universellt som Wilkins hade föreställt sig. Ironiskt nog föll Wilkins universella mått på att det inte var universellt nog, och arbetet med ett universellt, naturligt måttsystem rann ut i sanden.

Först i och med franska revolutionen – med dess ideal om frihet, jämlikhet och broderskap, om ett samhället byggt på upplysningens idéer, där vetenskapen och förnuftet hade ersatt religionen – väcktes åter tanken om ett nytt måttsystem. Diplomaten Talleyrand blev den som 1790 återuppväckte Wilkins idé om en universellt meter, definierad med en sekundpendel. Metern skulle definieras som pendelns utslag i Bourdeux, men därmed hade den mist lite av sin universalitet. Förslaget röstades också ned av den franska nationalförsamlingen.

Den franska folkförsamlingen, här samlad i en tennislokal och avbildad av Jacques-Louis David, bildades för att styra Frankrike efter revolutionen. Året efter revolutionen framlade den berömde diplomaten Talleyrand för folkförsamlingen sitt förslag om att införa pendelmetern, nu definierad som längden av en pendling uppmätt i Bordeaux. Trots internationellt bifall, inte minst från Storbritannien och de nygrundade förenta staterna dog förslaget snabbt ut.

Året efter, 1791, tillsattes därför en kommitté, som under ledning av matematikern Jean-Charles Borda skulle utarbeta en universellt giltig definition av den nya metern. Borda avfärdade alla definitioner som tog hjälp av pendlar, eftersom sekundpendeln utgick från den gamla sekunden, inte den nya som revolutionärerna definierat (där det skulle gå 100 000 nya sekunder på ett dygn). Istället bestämde man sig för att hela Jorden skulle få utgöra grunden för revolutionärernas nya mått. Den nya metern, beslöt man, skulle motsvara en tiomiljontedel av avståndet mellan nordpolen och ekvatorn. Problemet den här gången var att det var på tok både för dyrt och för farligt att resa till ekvatorn, och nordpolen hade ännu ingen besökt.

En approximation räddade det nya förslaget. Det är nämligen så, att fortet på berget Montjuïc i Barcelona ligger så gott som rakt söder om Paris, liksom klocktornet i Dunkerque ligger rakt norr om huvudstaden. Avståndet som skiljde dem var dessutom nära nog exakt en tiondel av hela sträckan från ekvatorn till nordpolen, det vill säga i moderna mått omkring tusen kilometer.

Uppdraget att mäta avståndet mellan Montjuïc och Dunkerque gavs åt två astronomer, Pierre Méchain och Jean-Baptiste Delambre. Méchain och Delambre skulle därefter tillbringa sex år, fram till 1798, med att resa genom ett Frankrike i storm för att mäta upp Jordens storlek. Till sin hjälp hade de ett instrument som uppfunnits av Jean-Charles Bordas assistent, Etienne Lenoir, redan flera år innan revolutionen.

Kyrktornet i Rodez dominerar fortfarande stadens horisontlinje. Efter att ha delat upp sträckan mellan sig var det här, på halva vägen, som Méchain och Delambre till slut möttes. Foto: Alain Pauziès, CC-BY-SA 3.0

De båda astronomerna delade upp arbetet emellan sig; Delambre skulle mäta sträckan från Dunkerque till Rodez och Méchain skulle mäta sträckan mellan Rodez och Barcelona. Med hjälp av två nyuppfunna instrument bestämde de avståndet från kyrktorn till kyrktorn genom hela Frankrike. Metoden de använde, triangulering, som du kan läsa mer om i det här inlägget. När mätningarna efter många äventyr, om vilka det står att läsa i Ken Alders bok Världens mått, var klara, adderades de bådas resultat och en meterstav av platina tillverkades. Nyheten om det nya måttet spreds därefter ut över Frankrike.

Trots alla Delambres och Méchains noggranna beräkningar hade dock ett fel smugit sig in. Efter Méchains för tidiga död kunde Delambre konstatera att kollegan uppe på Montjuïc gjort en felaktig mätning. Orsakerna gick aldrig att klarlägga, för den noggranne Méchain verkade ha gjort allting rätt. I desperata försök att rädda meterprojektet sitt misstag försökte han rätta till resultaten och därefter, när det misslyckades honom, att dölja felen. Fransmännen skulle fortfarande få veta att metern var en tiomiljontedel av Jordens omkrets – revolutionens löfte om ett samhälle byggt på en ofelbar vetenskap fick inte urholkas.

Delambre lade sig vinn om att inte framställa kollegans misstag som någon skandal. Därefter gick han vidare till att bli en av 1800-talets mest framstående franska matematiker och författare till flera böcker. Men, som Ken Alder skriver, "enligt Gauss var dessa senare verk livlösa och hantverksmässiga, matematiskt förenklade och i avsaknad av begreppslig elegans. De var med andra ord läroböcker."

Efter ett antal tumultartade revolutionsår besteg Napoleon år 1804 Frankrikes tron. Både som kejsare och som sekulär katolik ville han återupprätta relationen mellan Frankrike och den katolska kyrkan, som av förståeliga skäl tagit sig en rejäl törn under revolutionen. Ett av de mer underhållande problemen man mötte på var att revolutionärerna helt sonika avskaffat söndagarna – sedan revolutionen bestod ju veckorna av 10 dagar och ingen av dem hade reserverats åt kyrkan. Följaktligen återinfördes den gamla kalendern. Näst i tur stod de nya måttenheterna, som visserligen hade enat Frankrike, men också bidragit till att det isolerades från övriga Europa. Med en kejsares makt avskaffade Napoleon även metersystemet – året var då 1811. En nation av lättade fransmän kunde därefter återgå till de gamla enheterna.

Många var det nog som trodde att man med metersystemets avskaffande hade sett slutet på en parentes i mänsklighetens historia. Allt hade varit en utopisk dröm om ett revolutionärt måttsystem, framkastad av revolutionärer i revolutionärernas tidsålder. Tjugo år senare var så revolutionen förbi, dess slagord och galenskap glömd och måttsystemet dött och slutligen även på väg att begravas.

Även inom Frankrikes gränser tog befolkningen ibland god tid på sig att vänja sig vid metersystemet. Vid sekelskiftet mellan 18- och 1900-talen klagade en präst på att invånarna  i Corrèze, där bland annat vyn på bilden kan ses, fortfarande inte kände till metersystemet och ännu använde invånarna i Delambres hemstad Amiens de gamla enheterna för att mäta upp tyg. Foto: Wikimediaanvändare Mossot, CC-BY-SA 3.0

Men under loppet av 1800-talet skulle mycket komma att förändras. Industrialiseringen och järnvägen gjorde avstånden kortare och behovet av enhetliga mått långt mycket tydligare. Dessutom var uppfattningen om den enade nationalstaten på uppgång – perioden skulle se både Tysklands och Italiens enande – och ett enat land behövde ett enat måttsystem. Plötsligt började flera europeiska länder snegla på den franska revolutionens måttenheter i sin jakt på ett neutralt, vetenskapligt och modernt måttsystem. Först ut var Belgien, vars kung Vilhelm I av Oranien redan 1820 gjorde användningen av metersystemet tvingande; strax därefter följde Frankrike själv. I de nya, självständiga länderna i Sydamerika infördes också metersystemet, efter att den före detta kolonialmakten Spanien 1849 beslutat om dess införande.

I övriga Europa gick det desto mer trögt. I vägen stod för det mesta nationella intressen – där vissa menade att metern var baserad på Jordens omkrets och därmed fullständigt neutral, menade andra att allt den egentligen stod för var en fransk platinastav i ett franskt valv, dessutom felaktigt uppmätt av en fransk vetenskapsman. Samtidigt innebar fler nationer också fler åsikter. Krav började ställas från andra länder att metern skulle uppdateras. Metern hade nämligen avlägsnat sig mer och mer från den tiomiljontedel av Jordens omkrets den ursprungligen hade definierats som, allteftersom vetenskapen fortskridit med noggrannare mätningar. Förslaget ratades visserligen och den föreslagna förlängningen av metern uteblev, men till fransmännens kluvna förfäran blev den franska metern allt mindre fransk.

Vid världsutställningen i London 1851 hade domarna klagat på att mängden av olika måttsystem gjorde deras arbete omöjligt. Vid världsutställningen i Paris 1867 tog fransmännen därför tillfället i akt och visade upp metersystemets alla fördelar. Här ses Napoleon III dela ut pris till utställningens bästa bidrag.

Man kan se metersystemets popularitet i Frankrike som tvådelad. Å ena sidan fanns en önskan om att metersystemet skulle breda ut sig och att fler länder skulle ansluta sig till en franskledd måttunion, hellre än att de gick med i den konkurrerande brittiska; å andra sidan levde en rädsla om att andra länder, i synnerhet Preussen, skulle försöka ta metern i egna händer och i värsta fall försöka omdefiniera den – i praktiken skulle det ju innebära att Frankrike blev tvunget att erkänna att den franska metern från första början hade varit helt felaktig. Med anledning av denna rädsla motsatte sig Frankrike också alla försök att gjuta om meterstaven – risken var alltför stor att någon skulle försöka rätta till den.

Först efter kriget mellan Tyskland och Frankrike som avslutades 1871 gick Frankrike med på att gjuta upp nya meterstavar. Den franske kejsaren tvingades abdikera efter en preussisk totalseger, men de tyska sändebuden försäkrade att ingen avsåg förlänga den franska metern. En ny gjutning av meterstaven kunde slutligen påbörjas, där varje land skulle få sin egen. Därefter valdes en av dem ut för att bli den sanna, mest definitiva metern, och franka staten donerade en byggnad att förvara den i. Byggnaden hade totalförstörts under kriget, och nu fick meterländerna, däribland det nyligen enade Tyskland, betala för dess återuppbyggnad.

1889 skickades de nya meterstavarna ut i världen – metersystemet hade redan vunnit stor spridning. Många europeiska nationer hade adopterat metern och många nyligen självständiga kolonier hade sökt överbrygga traditionella hinder med ett gemensamt måttsystem. Redan 1866 hade USA infört metern som föredraget men inte tvingande måttsystem. Till Indien kom metern strax efter självständigheten 1947. Längst dröjde Storbritannien själv, där metersystemet gradvis infördes under loppet av 1970-talet. Det oundvikliga hade dock påpekats tidigt, när den skotske geologen John Playfair 1807 med ett citat från Ovidius uppmanat sina landsmän att gå över till metersystemet: Fas est et ab hoste doceri – "Man skall lära även av en fiende".

Ekonomi på matematiska

Jag har kommit att se på matematiken som närmast sinnebilden av Platons idévärld, med vilket han menade den värld av samband och information som styr den värld som tingen – och världen – faktiskt existerar i. Av detta följer att matematiken är en upptäckt, funnen när vårt intellekt hittat sätt att systematisera, förstå och analysera vår omvärld. På så sätt tränger våra tankar igenom de faktiska tingen till de bakomliggande sammanhangen och generella dragen som finns gömda däri, en definition av matematik som kanske ligger närmare logik än den faktiska matte de flesta möter i skolan, även om det där skulle kunna finnas spår av denna matematiska upptäckt – exempelvis något så simpelt som de naturliga talens sammankoppling med ett, två, tre, fyra äpplen. Eller vad som helst – huvudpunkten är att vår omgivning går att räkna.

Motsatsen till denna uppfattning måste vara att matematiken är en uppfinning. Återigen att vårt intellekt funnit ett sätt att systematisera och klassificera i avsikt att förstå och på så sätt dra vittgående slutsatser. På så sätt skulle den matematik vi i så fall uppfunnit vara ett sätt att beskriva vår omvärld – och därigenom blir matematiken ett språk. Och liksom hos ett språk finns möjligheten att applicera detta i en stor mångfald av situationer – som i syften knutna till astronomi och kronologi likt medeltidens beräkningar av påsken (se detta inlägg) eller grekernas strävan efter att knyta vinklar och avstånd till varandra med kordafunktionen, beskrivet i detta inlägg. Således har matematikens utveckling även skett utanför vad som traditionellt betecknats som den matematiska vetenskapen. Och, givet att matematiken är att betrakta som ett språk, vore ju dettas motsats lika absurd som att svenska endast skulle användas inom svensk lingvistisk vetenskap. Den matematiska historien, i egenskap av ett språk eller verktyg, har alltså även skrivits utanför själva matematiken. De kanske mest självklara områdena där så skett är de naturvetenskapliga ämnena, i synnerhet fysik, men även samhällsvetenskaper har använt matematik som redskap.

Så är kanske tydligast för ekonomin, även om kända klassiska ekonomer som John Stuart Mill, delvis Malthus och Marx, för att nämna några, huvudsakligen använde verbal analys och historiska exempel. Även om den klassiska ekonomin huvudsakligen berodde på en induktiv metod, där kunskap drogs ur generaliseringar av verkliga skeenden, använde även de, naturligtvis, slutsatser dragna ur teori och antaganden. Den huvudsakliga skillnaden mot neoklassisk ekonomi, som följde därefter, var metoden och vart den användes. Den klassiska ekonomin fokuserade mer på att förklara och diskutera verkliga fenomen som pågick i samhället, det vill säga huruvida en stat bör göra si eller så eller varför priset på ull beter sig på ett visst sätt, även om det fanns exempel i den andra riktningen. Ett sådant är Says lag, som är mer generell, men inte nödvändigtvis behöver vara formulerad genom deduktiva resonemang (logiskt utvunnen ur teoretiska påståenden), och formulerad inte genom matematik utan i ord.

Anledningen bakom intresset för klassisk ekonomi är dess kontrast mot neoklassisk ekonomi. Skiftet mellan dessa är naturligtvis inte exakt, men kan bedömas ligga under de två sista decennierna av 1800-talet. Den neoklassiska ekonomin skiljer sig från den klassiska genom sin användning av matematik och deduktion. Exempelvis kom begrepp som olika slags nytta att användas och ekonomer började resonera sig fram från påståenden som att alla människor är rationella till slutsatser som sedan skulle kunna appliceras på den verkliga ekonomin. En sådan slutsats formulerades av den neoklassiska ekonomen Irving Fisher, vars formel brukar kallas för Fishers ekvation (so u mean it's fishy?) och skrivs vanligen

där M är penningmängden, V pengarnas omloppshastighet, P prisnivån i samhället och T alla transaktioner. Ett vanligt sätt att presentera formeln är att i en ekonomi i jämvikt, det vill säga V och T är konstanta, innebär en ökning av penningmängden M, vilket skulle kunna vara att Riksbanken trycker mer sedlar än som kasseras, att P måste öka – varor och tjänster blir dyrare. Fenomenet kallas inflation. Att Fisher knöt samman sin teori till en matematisk formel gjorde den generell och överskådlig, men samtidigt innebär det på gott och ont att teorin tas ur sin kontext, eller sammanhang. Trots det har mängden matematik i ekonomin bara ökat.

Även andra neoklassiska ekonomer under 1800-talet sysslade mycket med matematik, exempelvis Léon Walras, Antoine Cournot och Nicolas-François Canard, även om det stora genombrottet för matematisk ekonomi kommit under 1900-talet med ekonometri, generell jämviktsanalys och spelteori men även med användandet av avancerade datormodeller.

Men den kanske viktigaste konsekvensen av ekonomins matematiserande är nog att det inneburit att ekonomin bytt karaktär, från en samhällsvetenskap till en naturvetenskap. Man glömmer lätt hur beroende en undersökning av människan är av sin kontext, eller sammanhang. En människa är en så pass komplex varelse med så många olika, sammanflätade faktorer att ingenting blir överskådligt om vi inte klumpar ihop de flesta och kallar det för kontext. Ekonomin har i sin naturvetenskapliga anda skapat naturlagar – Says lag, Fishers ekvation, Moores lag och så vidare. Dessa är visserligen mönster och generaliseringar som hjälper oss att förstå och förutse vår omvärld, men att benämna dem lagar är kanske att gå steget för långt. Matematiken är ett fantastiskt verktyg för att skapa generaliseringar, men man får ta sig i akt, även generaliseringar kan gå för långt.

En annan kritik som riktats mot matematisk ekonomi är att den kan begränsa urval vid undersökningar, ekonomer väljer ogärna problem och frågeställningar vars svar inte nås genom användande av en redan utarbetad matematisk modell. I mycket högre grad än verbala resonemang är matematiska modeller kostsamma och svåra att utveckla, resultatet är att ekonomiska resonemang kan tendera att använda samma banor om och om igen, och kanske på så sätt nå ett svar med lägre förklaringsvärde än vad som egentligen kunnat uppnås.

Trots detta bör man inte endast se den negativa aspekten. Faktum är att matematik har en nästintill magisk förmåga att igenkänna mönster och samband att ställa upp och genomföra experiment utan att riskera att riskera någons liv – vad hade ekonomin varit utan statistik och BNP, för att inte nämna datorsimulationer?

För vidare läsning kring ekonomins idéhistoria rekommenderas De ekonomiska idéernas historia av Martin Kragh, som också är källan till ekonomin i detta inlägg.

(o)Logiska Symboler

Först och främst: Det här är inte ett seriöst inlägg.

Matematiken tycks genom åren ha fått fler och fler symboler. Operationer och relationer som förr skrevs med bokstäver har successivt fått egna krumelurer. Om än kanske inte riktigt symbolisk, har matten blivit ett symbolspråk. Medan de medeltida matematikerna exempelvis skrev x² med bokstäver har det blivit allt svårare efterhand som vi tvingats hantera vem vet längre hur många dimensioner. Detsamma gäller rottecken, deltan, kongruenser, pilar åt olika håll och kanter, matriser, mängdlära och, inte minst, logiska tecken. För så många som säger att matte är ett eget språk (kallat exempelvis matematiska), så vore det väl synd om den saknade så grundläggande ordförråd som "och","eller" och "inte"?

Men redan där stöter vi på problemen, för vad menas egentligen med ”och”, vad menas med ”eller” eller till och med vad menas med ”inte”? Om jag nu inte tar tre äpplen, betyder det att jag tar fler, färre eller inga? Kan jag ta fyra och säga att jag inte tar tre?

Skulle man ta fyra äpplen härifrån skulle nog Paul Gauguin bli besviken.

Skriftspråkets rikedom på tvetydigheter är både dess förtrollning och dess förbannelse. För vad vore livet om man inte kunde säga något och mena något annat? Oklarheterna gör att skrift- och i synnerhet talspråket blir så svårt att säga något exakt på, men samtidigt så lämpade att vara kreativ med.

Det uppkommer ett annat problem med ”eller”. Om någon frågar ”Skall du gå in eller ut?” så förväntas du troligen inte svara ”Javisst, både och!” vilket du enligt all matematisk logik mycket väl borde kunna – men ingen kommer att förstå dig. Kanske borde vi alla börja tänka logiskt?

Ytterligare problem (det är tydligen bara det logik består av) uppkommer när man skall definiera ”men”. Utsagan ”A men B” (t.ex. det är soligt men det regnar) betyder ju bokstavligen att båda gäller (solen skiner och regnet faller) men ändå innehåller den mer information – de är på något sätt motsatta, man skulle helt enkelt inte förvänta sig att båda gällde samtidigt, det kommer att regna i morgon med.

Detsamma gäller naturligtvis även för alla andra begrepp som skall översättas från vårt vanliga språk till matematiska. Därför har matematiken egna tecken och betydelser för dessa tre ord:

∧	och
∨	eller
¬	inte

Notera att vi nu kan skriva ett känt citat på (engelsk) matematiska:

2b∨¬2b

om man för en stund bortser från det faktum att detta rent stringent faktiskt betyder att man samtidigt kan både vara och inte vara. Var det förresten Schrödingers katt som gick förbi där borta?

De här tre tecknen, de booleska begreppen, har blivit väldigt användbara inom programmering även om de då av naturliga skäl skrivs med vanliga bokstäver. De ingår i en uppsättning tecken som klassificeras som satslogik. Tre prominenta namn i sammanhang med satslogiken är George Boole (som givit begreppen deras namn), Gottlob Friege och Bertrand Russel. Även andra delar av matematiken och logiken håller sig med egna tecken, och vissa, däribland kanske mest prominent är mängdläran, har inte ens brytt sig om att snåla på dem.

George Boole föddes 1815 i ett rött tegelhus Lincolnshire i England och dog 1908 på Irland. Liknar han inte Abraham Lincoln?

Tre geometriska problem

Personligen tycker jag att matematik är som bäst när enkla, okomplicerade frågor leder till avancerade resonemang som till slut blir till lika enkla, eleganta svar. Sådana problem var exempelvis de antika grekerna mästare på att formulera – utan avancerade beräkningsmodeller, numeriska metoder med oändligt många steg eller axiom som strider mot all mänsklig intuition. Tre sådana problem, typiska för den grekiska matematiken, har blivit berömda på grund av sin skenbara enkelhet. Alla skulle lösas med endast passare och onumrerad linjal.

De tre geometriska problemen är alla känneteckna de för den grekiska matematiken, men i många fall är deras exakta uppkomst höljd i historiens dimma. Hippokrates, känd för sina insatser på medicinens område men även som författare till matematiska verk, står bakom en berömd sammanställning av problemen. Här ses ruinerna efter läkekonstens tempel, Asklepieion, på hans hemö Kos. Foto: Wikimediaanvändare Cup of coffee, CC-BY-SA 3.0

1. Vinkelns tredelning eller att dela en vinkel i tre lika delar
Att dela en vinkel i två lika stora vinklar är relativt enkelt, till och med med de sparsmakade verktyg grekerna ställde till vårt förfogande - man kan rent av bevisa att alla vinklar går att dela på mitten med de förutsättningarna. Att dela samma vinkel i tre lika stora delar är desto mer utmanande. Bortsett från ett antal speciella vinklar (3π/2, 9π/4, ja, alla som är en jämn tre-multipel av en konstruerbar vinkel) så krävs för tredelning av en vinkel ett speciellt villkor, som grekerna hade lika svårt för som de hade för siffran noll: Oändligheten.

Vem som först formulerade problemet med vinkelns tredelning är inte känt. Hippokrates, som intresserade sig för de tre problemen, visade däremot att det är möjligt att dela vilken vinkel som helst i tre delar om man har tillgång till en linjal med avståndsmarkeringar. En vinkel CAB kan då med tre steg delas i tre delar:

1. Dra ett streck rakt ned från C, så att det skär linjen AB i punkten D.
2. Fortsätt så att en rektangel bildas, genom att rita till linjerna CF och AF.
3. Rita ett streck AE, så att CHG och CGE blir likbenta trianglar, och HG, GC och GE lika långa som AC. Vinkeln BAG är nu en tredjedel av CAB.

En utförlig beskrivning av Hippokrates lösning på problemet, tillsammans med andra berömda matematikers lösningar, som Arkimedes, Nicomedes och Apollonius, står att finna på den här sidan.

Antagligen var det just eftersom problemet var så lätt att lösa med en numrerad linjal, som det ursprungliga problemet att dela vinkeln med endast en omarkerad linjal sällan fick någon uppmärksamhet. 1837 publicerade fransmannen Pierre Wantzel ett bevis för att det är omöjligt. Även om vissa vinklar går att dela i tre, finns ingen metod som kan dela alla vinklar, så till vida att man inte kan tänka sig att hålla på i all oändlig framtid. Vi som inte vill det får helt enkelt nöja oss med att tredelning är en redigt svår nöt att knäcka.

Problemet med tredjedelar återfinns redan i den mesopotamiska historien om Gilgamesh, som sades vara två tredjedelar gud och en tredjedel människa. Tror man att babylonierna visste om att det krävs oändligt många generationer för att åstadkomma det kan man tolka det som en subtil symbol för, exempelvis, att gudaätten skulle vara oändlig. Tror man inte på den tolkningen, så framstår det som att även de bästa kan göra matematiska felsteg, och att vissa felsteg verkar kunna leva kvar i tusentals år.

2. Cirkelns kvadratur eller att skapa en cirkel med samma area som en kvadrat
Det andra problemet är utan tvivel det äldsta av de tre - intresset för cirkelns area är lika gammalt som civilisationen själv. Svårigheten att från en cirkel skapa en kvadrat med lika stor area är ju ett problem som möter varje person som vill beräkna en cirkels area, eftersom alla areor jämförs i termer av kvadrater (vilket ju är varför vi överhuvudtaget talar om kvadratmetrar).

Den egyptiske skrivaren Ahmes, som står som författare till den berömda Rhindpapyrusen, lär ha givit anvisningen att ta bort en niondel från cirkelns radie och därefter konstruera en kvadrat med den sidan, men den förste som gav sig på att lösa problemet mer exakt var greken Anaxagoras, som enligt den alltid så välinformerade Plutarchos lär ha sysselsatt sig med problemet under tiden han satt i fängelse. Problemet var tydligen populärt bland de antika grekerna, såväl bland matematiker som icke-matematiker - faktum är att det omnämns i den samtida teaterpjäsen Fåglarna av Aristofanes.

Ifall Anaxagoras kom till någon slutsats är inte längre känt. Problemet blev under tiden mycket omtyckt i Grekland, men likväl upptäcktes ingen elegant och enkel lösning på problemet, som bara använde en omärkt linjal och passare. Faktum är att det gick så långt att grekerna började använda beteckningen cirkelkvadrerare för alla dem som utan framgång försöker göra det omöjliga.

Det intressanta med den här tidens lösningar på problemet är att de gick ut på att fylla cirkeln med trianglar eller rektanglar av allt mindre storlek - till slut, tänkte man sig, skulle månghörningen helt fylla cirkeln. Därefter var det lätt att sätta samman dem till en kvadrat och därmed ha löst problemet. Även om metoden fick kritik inte minst från Aristoteles, kan vi i efterhand konstatera att den egentligen var långt före sin tid. Tanken att en area kan beräknas genom att fylla den med oändligt många regelbundna rektanglar och trianglar av allt mindre storlek är inte många steg från 1600-talets integralkalkyl.

En av dem som konstruerade en sådan lösning var filosofen och retorikern Antifon från Aten. Han började med att placera en så stor kvadrat som möjligt i mitten av cirkeln, och fyllde därefter på med allt mindre rätvinkliga trianglar. Metoden återanvändes långt senare av Arkimedes för att ge ett närmevärde till π.

Antifon trodde att [cirkelns] area på detta sätt skulle fyllas, varför vi vid något tillfälle skulle ha en månghörning inskriven i cirkeln, med så små sidor att de skulle sammanfalla med cirkelns omkrets. Och, eftersom vi redan till varje månghörning kan skapa en lika stor kvadrat ... kan vi då också skapa en kvadrat lika stor som en cirkel.” - Simplikios från Kilikien

Staden Elis ligger i en dalgång på Peloponnesos västkust och var hemstaden för Hippias, vars bidrag till matematiken bland annat inkluderade den geniala quadratrix-kurvan med vars hjälp problemet med cirkelns kvadratur nästan kunde lösas. Till staden hörde även antikens Olympia, platsen för de antika olympiska spelen. Här ses den valvförsedda ingången till den antika arenan. Foto: Troy McKaskle, CC-BY-SA 2.0

Det stora genombrottet i lösningen av cirkelns kvadratur kom med matematikern och filosofen Hippias från Elis. Kring år 420 f.Kr. konstruerade han en kurva, som senare har kommit att bli känd som Hippias quadratrix, med vars hjälp han kunde härleda en lösning till problemet med vinkelns tredelning. Någon generation senare visade Deinostratos, en av Platons lärjungar, att den gick att använda även till att lösa problemet med cirkelns kvadratur. Haken med den här metoden var att quadratrixen i sig inte kunde konstrueras med enbart en passare och en omärkt linjal.

För att konstruera Hippias quadratrix behövdes ett särskilt instrument, som bestod av två stavar och en kvadrat. Den ena staven satt fast i kvadratens sidor, på så sätt att den kunde skjutas uppåt och nedåt, medan den andra var fäst i ett av hörnen och med en glidande infästning i den andra staven. Skärningspunkten mellan dem skapade quadratrixen. Bild: Wikimediaanvändar Kmhkmh, CC-BY-SA 3.0

Kan vi med dagens matematik till hjälp lösa problemet med cirkelns kvadratur? För att göra det, behöver vi först betrakta proportionen mellan en kvadrats sida och en cirkels radie. En kvadrat med sidan s har arean s², medan en cirkel med radien r har arean πr². Om vi vill skapa en cirkel med samma area som en kvadrat, får vi först sätta areorna lika, d.v.s.

För att få fram cirkelns radie måste alltså sträckan delas med kvadratroten ur π. Problemet är att roten ur π, liksom π självt, är tal går inte att skapa med de verktyg som grekerna ställde till vårt förfogande. På ett sätt var det just det problemet var det som Arkimedes mötte på, och anledning till att han använde Antifons metod för att skapa en approximation till π. Ytterst beror det på att π är ett s.k. transcendent tal, något som bevisades av matematikern Ferdinand von Lindemann år 1882, vilket i korta ordalag betyder att det inte är en lösning till någon algebraisk ekvation - fast det är en annan historia.

3. Kubens fördubbling eller att bestämma sidan på en kub som är dubbelt så stor som en annan kub
Det tredje problemet är troligtvis det yngsta av de tre problemen. Uppgiften är att att till en kub med känd sida och volym skapa en kub med dubbla volymen. Ganska snart började dock problemet cirkulera i en mer generell form: Att till en given kub konstruera en ny kub, vars volym förhåller sig till den gamla kubens volym med samma proportion som två givna linjers längder förhåller sig till varandra.

Av de tre geometriska problemen var detta det under antiken mest berömda, fast var med anledning av en anekdot om när Aten drabbades av pesten känt som det deliska problemet. Den mest underhållande, men knappast sanningsenliga, versionen av anekdoten ger den hellenistiske matematikern Theon från Smyrna, som återberättar en historia från Eratosthenes numer förlorade verk Platonikos. Han berättar, att när Atens invånarna frågade oraklet på Delos hur de skulle bli av med pesten fick de svaret att de i Apollons, tillfrisknandets gud, tempel skulle konstruera ett nytt altare, som var dubbelt så stort som det gamla. Byggmästarna, vars uppgift ombyggnationen blev, hade ingen aning om hur de skulle gå till väga för att uppfylla gudens önskningar, och rådfrågade därför i sin förvirring Platon. Denne vise herre svarade att guden i själva verket inte alls var intresserad av ett dubbelt så stort altare. Istället ville guden göra grekerna skamsna för deras ointresse för matematiken och motvilja mot geometrin.

Oraklet på Delos meddelade atenarna att de skulle bli av med pesten om de konstruerade ett nytt altare, som var dubbelt så stort som det gamla. Anekdoten fick sedan ge namn åt problemet med kubens fördubbling. Pesten som drabbade Aten år 430 f.Kr. hade dock ingen likhet med medeltidens böldpest. Vissa forskare menar istället att atenarna drabbades av tyfus, medan andra hävdar att sjukdomen under de millennier som gått antingen dött ut eller förändrats så mycket att vi inte längre kan känna igen den. Rykande färsk forskning föreslår att det egentligen rörde sig om ett tidigt utbrott av ebola. Notera dock att Platon, som ju är del av anekdoten, år 430 f.Kr. ännu inte var född. Tavlan ovan har målats av den flamländske konstnären Michiel Sweerts.

Det första genombrottet i lösningen av det deliska problemet stod Hippokrates för. Genom en genial upptäckt kunde han reducera problemet till att från två givna linjer, a och b, finna två linjer x och y, sådana att proportionen mellan a och x är densamma som den mellan x och y respektive y och b, eller med modern matematisk notation:

Hur kom då Hippokrates fram till att de två problemen egentligen var ett och samma - att man genom att lösa det ena, också hade löst det andra? Med modern matematik går det relativt enkelt att uttrycka:

Det säger oss att en kub med sidan a, som har volymen a³, förhåller sig till en kub med sidan x, som har volymen x³, på samma sätt som a förhåller sig till b. På så sätt kommer volymen av kuben med sidan a att förhålla sig till kuben med sidan x på samma sätt som linjen a förhåller till linjen b. Uppgiften kan därför förenklas till att från två givna linjer a och x skapa linjerna y och b. Vårt resonemang bygger dock på modern matematik - hur Hippokrates kom fram till samma slutsats får förbli ett mysterium att förbrylla de lärda.

En gång trodde man att man hittat matematikern Archytas skulptur i Villa dei Papyri i Herculeanum nära Pompeji. Senare visade sig statyn istället avbilda Pytagoras. Till villan hörde en gång ett stort bibliotek, som begravdes under askan från vulkanen och på så sätt blivit det enda bevarade antika biblioteket. Mycket av vår kunskap om antiken kommer från de dokument som hittats under utgrävningarna. I romersk tid var villan en samlingsplats för människor som följde den grekiske filosofen Epikuros läror, där filosofiska diskussioner och gott sällskap alltid stod högt i kurs. Foto: Dave Hill och Margie Kleerup, CC-BY-SA 2.0

Det allra största genombrottet vad gäller det deliska problemet kommer dock från en annan antik matematiker, Archytas. Hans upptäckt förbättrades sedan av en annan matematiker, Menaichmos, också han en vän till Platon och dessutom bror till Deinostratos, som löste problemet med cirkelns kvadratur. Archytas lösning är anmärkningsvärd, som Thomas Heath skriver i boken A history of Greek mathematics, "especially when his date is considered (first half of fourth century B.C.), because it is not a construction in a plane, but a bold construction in three dimensions".

Genidraget i Archytas lösning är hans insikt, att skärningspunkten mellan en parabel och en hyperbel skapar en kurva, som vrider sig i tre dimensioner. Med andra ord går den inte att rita ut på ett papper. I Gauss ord är kurvan negativ, men till den tiden skulle det dröja mer än två millennier. En fullständig beskrivning av Archytas lösning kan läsas i Thomas Heaths bok (sid. 246-249), eller i sammandrag på den här hemsidan.

Att den är slående, det är nog det minsta man kan säga om Archytas lösning - det är en komplicerad konstruktion i tre dimensioner, där halvcylindrar och koner trängs med ellipser och cirklar; allt för att konstruera de linjer x och y som Hippokrates anbefallt. Till och med i ett modernt 3D-program är Archytas konstruktion svår att genomskåda - frågan är hur han själv inte bara lyckades föreställa sig en sådan figur, utan även kunde dra slutsatsen att han därigenom hade konstruerat rätt längder.

Hur magnifikt genial Archytas lösning än må vara, kan den inte kringgå den grundläggande svårigheten som gör alla de tre problemen olösliga. Det gäller för π, som i problemet med vinkelns tredelning, och för roten ur π, som i problemet med cirkelns kvadratur, som Pierre Wantzel visade på 1830-talet, men även för kubikroten ur två, som i det deliska problemet. Som den siste store företrädaren för pytagoréernas matematik, måste Archytas ha känt den starkaste frustrationen inför dessa irrationella tal. Problemet är dock inte i sig att talen är irrationella - pentagrammet går trots sina irrationella sidor mycket bra att konstruera geometriskt, något som Euklides visade i sin Elementa. För att konstruera kubikroten ur två krävs däremot en figur i tre dimensioner, vilket var precis vad Archytas levererade. I ett plan, d.v.s. begränsat till två dimensioner, är det - per definition, eftersom kubikroten har just med volym att göra - omöjligt.

Trots det fick alla de tre problemen till slut sin lösning av geniala matematiker och filosofer i Platons generation. Att de fortfarande betraktades som olösliga, beror på att grekerna hade rangordnat de olika lösningsmetodernas elegans. Bäst var de så kallade platonska lösningarna, som skulle genomföras i ett plan med bara passare och omärkt linjal. Därefter kom lösningar med kägelsnitt, som ellipser och parabler. Minst eleganta ansågs de lösningar, där det behövdes ett speciellt verktyg, som Hippias quadratrix-instrument.

Med en vidare definition kan, som grekerna själva visade, alla de tre problemen lösas. Origami är ett annat, kraftfullt alternativ. På sätt och vis var det alltså inte problemen i sig som var omöjliga, utan grekerna själva. Genom Platons idealism, vars popularitet bara skulle stiga, uteslöt de alla möjliga lösningar, och låste sig vid att finna de omöjliga. Samtidigt som de formulerade enkla och eleganta problem, kan man säga, att de i sin jakt på elegans satte på sig sin egen ögonbindel.

Historien om två målare som skulle måla en trumpet

Först tänkte jag återberätta vad som kan kallas en "matematisk rolig historia", eller åtminstone en paradox.

Om man tar kurvan till y=(1/x), vilket är ett mycket vanligt exempel på en asymptot (dvs. en kurva som närmar sig en linje utan att någonsin nå den, i det här fallet linjerna x=0 och y=0), och ritar upp den för x>1 så blir resultatet en backe som börjar i y=1 då x=1 och får y=0 då x når oändligheten.

Roteras denna kurva kring x-axeln, så att en rotationskropp skapas, blir resultatet en oändligt lång trumpet. Men eftersom matematikens natur så är denna kurva färglös sätter vi två målare på att måla den i en dyr djupblå kulör. De får vardera en burk färg, och måste måla hela kurvan, ända bort till oändligheten. Om den ena får i uppdrag att måla kurvan med pensel, medan den andra får i uppdrag att fylla kurvan med blå färg - vem förbrukar mest av den dyra färgen?

Det självklara och intuitiva svaret på den här frågan är naturligtvis den som fyller kurvan (det måste väl gå åt mer om man fyller kurvan än om man bara målar dess sidor?) - trots att jag redan från början skrev att det var en paradox. Det rätta svaret är därför att den som målar med pensel förbrukar mest färg.

Att måla trumpeten betyder att målaren måste gå längsmed hela kurvan, och måla varje halvmeter med penseln för sig. Oavsett hur snål och sparsam målaren är med färgen, kommer förbrukningen att vara i evigt, eftersom kurvan är oändligt lång. Den som skulle fylla kurvan å andra sidan behöver bara stå på ena sidan, och eftersom arean under en 1/x-kurva är möjlig att bestämma matematiskt, det vill säga att den är begränsad och har ett värde, kan vi avgöra hur mycket färg den här målaren kommer att förbruka.

Formeln för längden av en kurva är

eller mer specifikt för vårt fall (nu multiplicerad med radien 1/x och 2 π eftersom det är arean av kurvan vi vill åt)

Denna integral går mot oändligheten, varför målaren som målar med pensel aldrig kommer att bli klar. "Volymen" på "trumpeten" bestäms av en vanlig integral insatt i formeln för en cylinders volym (eftersom trumpeten i grund och botten är en mycket uttänjd och ihopdragen cylinder, där höjden har ersatts med en annan, icke-horisontell funktion) och målaren som fyller trumpeten kommer att bli klar ganska snart. Volymen är nämligen begränsad enligt

hur otroligt det än må låta. (Enheten här är volymenheter, men beror av vad som ansätts på axlarna.)

Formeln som jag använde för att bestämma kurvans längd är egentligen höjdpunkten (inte ens jag märkte det) i dagens inlägg. Den härleds genom att man väljer ett litet delta-x (jag tänker inte ge mig på att skriva den grekiska bokstaven delta här och nu) och får därför ett delta-y. Om man använder Pythagoras sats på dessa får man en delta-längd på kurvan uttryckt i x och/eller y. Med lite förenkling och integration har man formeln. Detsamma gäller ifall man önskar den för ett polärt koordinatsystem.

Den formeln är ett ganska så kraftfullt verktyg, även om den innehåller en kvadratrot som gör den svår att lösa exakt. I fall som dessa gör sig därför numeriska integraler ganska väl.

Det gyllene snittet under fem tusen år

Hunden, människans bäste vän? Inte då, det gyllene snittet låter sig inte besegras så lätt! "De lyckliga hundarna" av Richard Ansdell.

Alltsedan de kambriska havens värld har det funnits snäckor, anfäderna till dagens snäckor, de snäckor vars skal urmänniskorna plockade och beundrade längs stenålderns havsstränder, och de besitter en matematisk hemlighet. Fast deras koppling till det gyllene snittet är nog inte så vidare hemlig längre. Fortfarande, efter att ha levt i en värld där vi ser det gyllene snittet varthän vi än vänder våra ögon, verkar det aldrig upphöra att fascinera oss. Kanske är det just därför vi dras till det, kanske är det vår världs emblem. Och mer exakt är talet ett plus kvadratroten ur fem genom två, eller det gyllene snittet.

Att både snäckor och kottar, lika väl som solrosor och myriader av andra ting i naturens värld går att hänföra till det gyllene snittet var kanske just den inspirationskälla som ligger till grund för den konst och matematik som följt i dess spår. Både som proportion, det gyllene snittet, och som sidorna på en rektangel, den gyllene rektangeln, har talet följt med oss sedan urminnes tider. Rektangeln lär vara den skönaste möjliga, utvald av människor i alla kulturer. Och då måste den vara ett framgångsrecept för den som vill skapa slående konst.
Somliga tror att redan de gamla egyptierna kom underfund med detta i sitt sökande efter en byggnad som kunde överskrida barriären till livet efter detta - den som ställer sig mitt på en av pyramidernas sidor, förväntas komma fram till att avståndet till toppen, längs med ytan, förhåller sig med det gyllene snittet till tre decimalers noggrannhet till avståndet till pyramidens centrum. För den äldsta befästa användningen av det gyllene snittet får vi dock vänta ytterligare ett och ett halvt millennium, till det antika Grekland.

Gyllene snittet eller inte, ligger pyramidernas skönhet i deras matematik?

Man kan säga, att den grekiska matematiska traditionen sträcker sig från Thales från Miletos, via hans lärjunge Pythagoras och Pythagoras lärjungar tills Sokrates, Platon och Aristoteles. Däremellan finner vi Euklides, och, runt den tid då Parthenon på Akropolis i Aten uppfördes, skulptören Fidias. Fidias betraktades redan av romarna som en av Greklands mest briljanta konstnärer, med både ett av den antika världens sju underverk bland sina skapelser och de två statyerna av Athena, staden Atens skyddsgudinna, som då prydde templet, och deltog i att göra det världsberömt. Hans verk lever idag endast genom kopior, varav de flesta gjordes under romersk tid, men minnet av honom har idag fått en återfödelse genom att man under 1900-talet lät den första bokstaven i hans namn, den grekiska bokstaven φ, fi, beteckna den proportion som var pionjär med att använda. Det gyllene snittet skrivs därför ofta

Pythagoréerna höll det gyllene snittet som en gudomlighet i sin av talmystik uppbyggda världsbild, liksom π, men blev av båda djupt besvikna, när det upptäcktes att de var irrationella, och således gick på kors med en annan av pythagoréernas grundprinciper, att alla tal kan skapas genom att dela två heltal med varandra. Den uppfattningen fanns för övrigt i stort i hela det antika grekiska samhället, och det var därför inte så märkligt att grekerna vände sig till bråken när de försökte uttrycka tal som pi eller det gyllene snittet i siffror. Idag brukar vi ju benämna dem approximationer, men jag skulle kunna tänka mig att de antika grekerna i alla fall för en stund trodde sig ha funnit det exakta uttrycket. Likaväl kan man ju föreställa sig den antike grekiske matematiker som med ljus och lykta söker längsmed tallinjen av idel rationella tal; "Men det måste ju finnas någonstans här!". Men lika besvikna över det gyllene snittet som över pi behövde pythagoréerna inte bli; ett vanligt sätt att definiera det gyllene snittet på är faktiskt med hjälp av ett bråk:

där förhållandet a till b motsvarar det gyllene snittet, vilket man ser om man sätter in b=1, eftersom man då får a=φ; sätter man in b=2 får man a=2φ. Om man då just sätter in b=1 så får man istället en andragradsekvation, vars lösning är just det gyllene snittet:

Den visar på en av det gyllene snittets kännetecknande egenskaper, nämligen att φ i kvadrat är detsamma som φ+1. (Något man får fram om man adderar x+1 till vardera sidan.)

Ett fragment från en avskrift av Euklides Elementa från omkring 100 e.Kr., det matematiska grundverk som också innehåller den första matematiska beskrivningen av det gyllene snittet.

Den första matematiska beskrivningen av det gyllene snittet står dock att finna i Euklides Elementa, ett av matematikens absoluta grundverk. Euklides, utöver att han bland annat visade att det gyllene snittet är irrationellt, gav den kanske enklast möjliga geometriska definitionen av det gyllene snittet, den som inspirerade det matematiska uttryck som vi använde som startpunkt precis här ovanför. Euklides, som kallar proportionen för den ytterlighetens och medelvärdets förhållande, i fri översättning från engelskan, eftersom min antika grekiska tyvärr är i behov av allvarligt förbättringsarbete, definierar den genom att dra en rät linje och dela den i två, så att en kort och en lång del skapas. Han säger då att den korta förhåller sig till den långa biten med det gyllene snittet, ifall det råder samma proportion mellan dem, som det gör mellan den långa biten och hela sträckan. Rent och elegant, men i behov av en illustration:

Euklides definition av det gyllene snittet; där proportionen mellan a och b är densamma som proportionen mellan a och hela sträckan, a+b. Definitionen är fortfarande, med över två millennier på nacken, en av de mest använda.

Det skulle dock dröja mer än tolv hundra år innan en man upptäckte vidden av det gyllene snittets nära koppling till talens självaste natur; hans namn var Fibonacci. Boken han lät publicera år 1202 var banbrytande på många sätt (se detta inlägg), inte minst för den studie på kaniner han beskrev. Varje kanin, enligt Fibonacci, föder en ny kaninunge per månad, som tar en månad att växa upp innan den skaffar egna kaninungar. Onödiga komplikationer som att det måste vara två kaniner för att det överhuvudtaget skall bli kaniner skalade Fibonacci bort. En kaninunge kommer därför inte att skaffa någon kanin månad ett. Månad två gör den dock så, och då finns det två kaniner. Men den nyfödda kaninen är för ung, och nästa månad föds det fortfarande bara en kanin, och det finns tre kaniner. Men då finns det med en gång två kaniner som skaffar kaninungar, och nästa månad finns det fem kaniner, tre vuxna och två ungar. Följaktligen finns det månaden därpå fem kaniner, sedan åtta, tretton, tjugoett och trettiofyra. Fibonaccis talserie är skapad.

Men det förbluffande är fortfarande kvar; om man delar ett fibonaccital, som vi kallar F(n), med fibonaccitalet innan, F(n-1), får man, ju större fibonaccital man väljer, en kvot allt närmare phi, det gyllene snittet. Vi kan se att 2/1=2; 3/2=1,5; 5/3=1,66...; 8/5=1,6; 13/8=1,625; 1,61538...; och så vidare; 39088169/24157817=1,618033989... om x är kvoten mellan ett fibonaccital och det förra, så får vi

Beviset var dock inte Fibonaccis förtjänst, utan utformades av Johannes Kepler, ett århundrade senare. Ungefär samtidigt publicerades den första decimalapproximationen av det gyllene snittet, av Michael Maestlin, år 1597, istället för de bråk som grekerna försökte fånga det gyllene snittet i, och som Euklides visade var omöjligt, ändock är det lika omöjligt att skriva talet som ett decimaltal.

Under upplysningen fann man många exempel på det gyllene snittet i naturen, som gick väl i linje med tidens melodi: att världen är matematisk som ett klockverk. 1835 benämndes proportionen för första gången det gyllene snittet, istället för Euklides ytterlighetens och medelvärdets förhållande, och på nittonhundratalet fick Fidias ge namn åt förhållandet. Men det gyllene snittet ligger alltför nära vår värld för att försvinna med den deterministiska, förutsägbara och urverkslika världsbilden, och dyker upp till och med i Roger Penrose mönster och Dan Shechtmans Nobelprisbelönade kvasikristaller. Men det är en annan historia.

Är det gyllene snittet med och leder oss in i en fjärde rumsdimension? En legering av zink, mangan och holmium uppvisar ett oregelbundet mönster med det gyllene snittets proportioner. Bild: Wikimedia Commons-användare Materialscientist, CC BY-SA 3.0

För exempel på det gyllene snittets förekomst i geometrin, se den här externa sidan.

Ägg, påskharar och matematiska beräkningar

Nu närmar sig påsken med stormsteg och förhoppningsvis har värmen kommit för att stanna. Påsken infaller som bekant efter vårdagjämningen – det dygn då dag och natt är lika långa – nämligen, enligt tumregeln, den första söndagen efter den första fullmånen efter vårdagjämningen.

Påsken är en av kyrkoårets viktigaste högtider, och bristen på en gemensam dag att fira den på utgjorde ett problem för den tidiga kyrkans sammanhållning. Firandet har dock fått olika tema i olika länder, som denna bild från Santiago de Compostela. Foto: J. Pereira, CC-BY-SA 2.5

Men det var som sagt bara tumregeln. Verkligheten är som vanligt långt mycket mer komplicerad, och de munkar som under medeltiden hade för uppgift att beräkna påskens datum var ofta i den dåtida framkanten av matematiken. Beväpnade med Ptolemaios (ca 90-168 e.Kr) bild av solsystemet, med epicykler och jorden i centrum (se äldre inlägg här och här om denne briljante men ack så misstagne matematiker och astronom) och antik grekisk, medeltida bysantinsk, arabisk och europeisk matematik arbetade de fram tabeller över påskens datum långt in i framtiden.

Diskussioner om när påsken skulle infalla har förts åtminstone sedan mötet mellan påven Anicetus och biskopen Polykarpos av Smyrna år 154 e.Kr., men det var först vid det första konciliet i Nicaea (som idag ligger på Turkiets västkust) år 325 som den kristna världen fick ett gemensamt sätt att beräkna påsk. Då beslutades att hela kristendomen skulle använda det sätt som var bruk i Alexandria. Det tog dock flera århundraden innan hela den kristna världen accepterat bestämmelsen.

Denna illustration från 1493 av konciliet i Nicaea återfinns i den berömda Nürnbergkrönikan, som skildrar den kristna världens historia. Konciliet i Nicaea sammankallades av den kristne romerske kejsaren Konstantin, bland annat för att fastlägga påskens datum.

Det system som då infördes används fortfarande idag, fast på lite olika sätt. Först och främst delas året in efter en månkalender – året får tolv månader, på vardera vanligen 29 dagar – men ett sådant år är elva dagar för kort. Varje år kommer månkalendern alltså elva dagar till efter solkalendern. (Mån-månaderna definieras på så sätt att fullmånen – den formella fullmånen, som inte nödvändigtvis överensstämmer med verklighetens fullmåne – inträffar på månadens fjortonde dag.) När tre år gått och månkalendern ligger 11·3 = 33 dagar efter, skjuts en extra månad in på 30 dagar. De överskjutande dagarna blir alltså 33-30 = 3. Nästa år blir de elva till, året därpå och året därpå igen också, tills de överskjutande dagarnas antal når 3+3·11 = 36. En extra månad läggs till och, ja, dagarna minskas till 6. På det här viset upprepas processen tills de överskjutande dagarna är -1, d.v.s. tills månkalendern ligger en dag före solkalendern, något som inträffar på det nittonde året. Då läggs en skottdag in – då månen formellt sett står stilla – och kalendern börjar om. Därför går månkalendern i cykler om nitton år.

Den första månad i vilken den fjortonde dagen (dess formella fullmåne) i denna månad hamnar på eller efter vårdagjämningen den 21 mars är påskmånaden och den första söndagen efter den fjortonde dagen i denna månad är då påsken infaller. Påsken infaller som tidigast om den fjortonde dagen i någon mån-månad är just den 21 mars, samt detta är en lördag. Söndagen som följer därpå måste alltså bli påsk, som således inträffar den 22 mars. Om å andra sidan påsken inträffar den femtonde i denna månad väntar påskmånaden till nästa månad, och dess fjortonde dag blir då den 18 april. Om denna dag vidare själv skulle vara en söndag, väntar påsken till nästa söndag, som blir den 25 april, vilket är det senaste datum påsken kan inträffa.

Eftersom vårdagjämningens datum (satt i solkalendern), månens formella fullmåne (fixerat till den fjortonde i varje månad i månkalendern) och veckodagarna här samvarierar, hoppar påsken fram och tillbaka i en cykel på nästan 6 miljoner år. Sannolikheten att påsken skall inträffa ett visst datum framgår av diagrammet. Är man osäker och skall gissa, förefaller stalltipsen vara den 19 april (och det med en hisnande säkerhet på nära fyra procent).

Det romerska talsystemet

Det romerska talsystemet har kommit att bli ett långlivat system. Med sina rötter i den norditalienska förhistorien, har det levat kvar och utvecklats genom antiken, medeltiden och renässansen, för att fram till vår tid leva sida vid sida med det indo-arabiska talsystemet. På vägen har mycket skett, som påverkat hur det använts och fungerat. Här syns talet 52 på en antik inskription på Kolloseum i Rom. Foto: Ben Mitchell, CC-BY-SA 3.0.

Det romerska talsystemet, som tvärtemot vad namnet antyder egentligen är mycket äldre än den romerska civilisation själv, är ett av vår världs äldsta ännu levande arv från det förgångna. Fortfarande, efter mer än tretusen år, är det i daglig användning i stort sett alla av samhällets områden, för att numrera alltifrån kungligheter till klockslag och närhelst annars de indo-arabiska siffrorna inte riktigt skulle passa. På sätt och vis är det därför märkligt att kalla de romerska siffrorna för romerska, dels för att de är äldre än romarna, och dels för de lika mycket är våra, som de inte egentligen är romarnas.

Principen bakom det romerska talsystemet är mycket enkel och har ett omfång på sju bokstäver, som vardera tilldelats ett siffervärde:

I	1
V	5
X	10
L	50
C	100
D	500
M	1000

På så sätt är det romerska talsystemet mycket platseffektivt när det kommer till att skriva höga, jämna tal, som t.ex. hundra eller tusen, medan mer ovanliga tal blir desto mer komplicerade. Om bokstäverna placeras i sjunkande följd skall de adderas, så att VI = 6, medan de skall subtraheras om de placeras i stigande följd, alltså IV = 4. Därför skrivs 558 som DLVIII, men 559 som DLIX. År 2000 är lätt att skriva, MM, till och med kortare än med indo-arabiska siffror, men 1492 blir desto längre, MCDXCII.

Det romerska talsystemets position var ohotad i vart fall fram till början av tolvhundratalet, då Leonardo från Pisa, mer känd under tillnamnet Fibonacci, publicerade sin bok Liber Abaci, där han – utöver att han uppfann världens säkerligen mest berömda talserie – för första gången introducerade den europeiska befolkningen till de indo-arabiska siffrornas krafter. (Fibonacci, hans siffror och deras väg från Indien till Europa kan du läsa mer om i detta inlägg.)

Tävlingar som denna från 1527, där en deltagare använde en abakus och romerska siffror (i det här fallet mannen längst till höger) och den andra papper och penna och indo-arabiska siffror (här mannen längst till vänster), var vanliga i den tid då de indo-arabiska siffrorna var nya. Man ville ta reda på vilket räknesätt som gav snabbast resultat, men framförallt säkerställa att båda svarade likadant. Misstron mot de nya siffrorna var utbredd – det var inte för inte som en förvirrad publik omvandlade arabiskans sifr, som betyder noll, det nya tal som följde med det indo-arabiska talsystemet, inte bara till siffra, utan också det mer nedvärderande chiffer.

Den grundläggande skillnaden mellan det indo-arabiska och det romerska talsystemet kan ses i ljuset av deras användningsområden. De romerska talen användes för att skriva ned saker, för att överföra eller bevara information, medan själva beräkningarna alltid gjordes på en abacus eller kulram. Användningen av kulramar var vitt spridd redan under romersk tid, då bläck och papper dessutom var något dyrt som inte användes i onödan.

Kraften i de indo-arabiska talen visar sig först när man börjar göra beräkningar med dem, när själva matematiken utförs i siffror på papper och inte med kulram. Introduktionen av indo-arabiska siffror är därför tätt kopplad till kulramens tillbakagång.

De nya talen, som när de kom till Europa redan under lång tid använts av indiska och sedan även arabiska astronomer, var inte bara ett talsystem för den tidiga medeltidens relativt enkla ekonomiska beräkningar, utan för matematisk akrobatik med trigonometriska funktioner och för de invecklade ekonomiska konstruktioner som började att uppkomma mot medeltidens slut. Plötsligt gällde handeln inte mynt eller får utan summor som skulle överföras från en valuta till en annan, procent av belopp, räntor och mycket annat. Som de medeltida matematikerna snart fick erfara var sådana övningar stort sett omöjliga att genomföra med de gamla, romerska talen.

Motståndet mot de nya siffrorna var dock stort även bland de som själva utförde sina beräkningar. För att möta de allt mer komplexa matematiska behov som började uppkomma utan att fördenskull släppa de gamla beprövade talen, började det tidigt att uppkomma olika slags anpassningar och tillägg, i många fall århundraden innan de indo-arabiska siffrorna blev kända. Inte minst krävdes redan på tidigt stadium avancerade astronomiska beräkningar för att bestämma påskens datum, något som under lång tid utgjorde en grundläggande matematisk stridsfråga (som du kan läsa mer om i det här inlägget). När beräkningarna började innehålla högre tal och fler tal, behövdes smidigare sätt att skriva dem på. Därför uppfann de medeltida matematikerna nya bokstäver, som O för 11 från franskans onze, N för 90, från latinet nonaginta, eller F för 40, från engelskans forty.

S, härlett från latinets septem, kunde stå för 7, men kunde från latinets septaginta lika väl betyda 70. Från det grekiska talsystemet lånade man stigma, Ϛ, med betydelsen 6. Den vördnadsvärde Beda, som levde och verkade i 700-talets England, förkortade latinets nulla, noll, till N, trots att bokstaven redan användes för att beteckna 90. Här ses han på en tavla av James Doyle Penrose från 1902 i färd med att översätta Johannesevangeliet.

Men Europa är stort och medeltidens människor talade än fler språk än vad vi gör idag, och eftersom många tal till råga på allt börjar på samma bokstav kom nog de nya tilläggen till det romerska talsystemet i längden att kosta mer än de smakade. För det romerska talsystemet kvarstod ändå en rad grundläggande problem:

1. Bråkräkningen var mycket mindre välutvecklad och i allt väsentligt härledd från romerska myntenheter.
2. Negativa tal, i den mån de ens gick att skriva, var klumpiga och lätta att missförstå.
3. Trots trevande försök saknades ett gemensamt sätt att skriva talet noll.

Kort sagt saknade det romerska talsystemet standardisering, utan varierade istället vilt från författare till författare och mellan olika platser. När handeln blev internationell och vetenskapen fortskred räckte det helt enkelt inte längre till. Numera finns det vissa regler även för det romerska talsystemet, men om man tittar noga på de antika siffrorna ser man att de reglerna inte alltid stämmer. Romarna skrev nämligen på känsla, och först i modern tid har man försökt att standardisera det romerska talsystemet.